Najděte a prozkoumejte extrémní body funkce. Druhý znak extrému funkce
Úvod
V mnoha oblastech vědy i v praktických činnostech se často musíme potýkat s problémem hledání extrému funkce. Faktem je, že mnoho technických, ekonomických atd. procesy jsou modelovány funkcí nebo několika funkcemi, které závisí na proměnných - faktorech ovlivňujících stav modelovaného jevu. K určení optimálního (racionálního) stavu a řízení procesu je třeba nalézt extrémy takových funkcí. Takže v ekonomii se často řeší problémy minimalizace nákladů nebo maximalizace zisku – mikroekonomický problém firmy. V této práci neuvažujeme o problémech modelování, ale uvažujeme pouze o algoritmech pro hledání extrémů funkcí v nejjednodušší verzi, kdy na proměnné nejsou kladena žádná omezení (nepodmíněná optimalizace) a extrém se hledá pouze pro jednu cílovou funkci.
EXTRÉMY FUNKCE
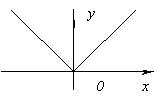
Uvažujme graf spojité funkce y=f(x) znázorněno na obrázku. Funkční hodnota v bodě X 1 bude větší než funkční hodnoty ve všech sousedních bodech jak nalevo, tak napravo X 1. V tomto případě říkáme, že funkce má v bodě X maximálně 1. Na místě X Funkce 3 má samozřejmě také maximum. Pokud vezmeme v úvahu bod X 2, pak je v něm funkční hodnota menší než všechny sousední hodnoty. V tomto případě říkáme, že funkce má v bodě X 2 minimálně. Stejně tak k věci X 4 .
Funkce y=f(x) na místě X 0 má maximum, pokud je hodnota funkce v tomto bodě větší než její hodnoty ve všech bodech nějakého intervalu obsahujícího bod X 0, tzn. pokud existuje takové okolí bodu X 0, která je pro všechny X≠X 0 , příslušnost k této čtvrti, nerovnost platí f(x)<f(x 0 ) .
Funkce y=f(x) Má to minimální na místě X 0 , pokud existuje takové okolí bodu X 0 , to je pro všechny X≠X 0 patřící do tohoto okolí, nerovnost platí f(x)>f(x 0.
Body, ve kterých funkce dosáhne svého maxima a minima, se nazývají extrémní body a hodnoty funkce v těchto bodech se nazývají extrémy funkce.
Věnujme pozornost tomu, že funkce definovaná na segmentu může dosáhnout svého maxima a minima pouze v bodech obsažených v uvažovaném segmentu.
Všimněte si, že pokud má funkce v určitém bodě maximum, neznamená to, že v tomto bodě má funkce největší hodnotu v celé definiční oblasti. Na obrázku diskutovaném výše je funkce v bodě X 1 má maximum, i když existují body, ve kterých jsou funkční hodnoty větší než v bodě X 1 . Zejména, F(X 1) < F(X 4) tj. minimum funkce je větší než maximum. Z definice maxima pouze vyplývá, že se jedná o největší hodnotu funkce v bodech dostatečně blízkých bodu maxima.
Věta 1. (Nezbytná podmínka pro existenci extrému.) Je-li diferencovatelná funkce y=f(x) má na místě x=x 0 extrém, pak se jeho derivace v tomto bodě stane nulou.
Důkaz. Pro jistotu k bodu X Funkce 0 má maximum. Potom pro dostatečně malé přírůstky Δ X my máme f(x 0 + Δ X)
Přechod v těchto nerovnostech do limitu v Δ X→ 0 a vezmeme-li v úvahu, že derivace F "(X 0) existuje, a proto limita vlevo nezávisí na tom, jak Δ X→ 0, dostaneme: při Δ X → 0 – 0 F"(X 0) ≥ 0 a při A X → 0 + 0 F"(X 0) ≤ 0. Od F"(X 0) definuje číslo, pak jsou tyto dvě nerovnosti kompatibilní pouze tehdy, když F"(X 0) = 0.
Osvědčený teorém říká, že maximální a minimální body mohou být pouze mezi těmi hodnotami argumentu, při kterých se derivace stává nulou.
Uvažovali jsme případ, kdy funkce má derivaci ve všech bodech určitého segmentu. Jaká je situace v případech, kdy derivát neexistuje? Podívejme se na příklady.
y=|X|.
Funkce nemá v bodě derivaci X=0 (v tomto bodě nemá graf funkce definovanou tečnu), ale v tomto bodě má funkce minimum, protože y(0)=0 a pro všechny X≠ 0y > 0.
nemá žádnou derivaci at X=0, protože to jde do nekonečna X=0. Ale v tomto okamžiku má funkce maximum. nemá žádnou derivaci at X=0, odkdy X→0. V tomto bodě funkce nemá ani maximum, ani minimum. Opravdu, f(x)=0 a při X<0f(x)<0, а при X>0f(x)>0.Z uvedených příkladů a formulované věty je tedy zřejmé, že funkce může mít extrém pouze ve dvou případech: 1) v bodech, kde derivace existuje a je rovna nule; 2) v bodě, kde derivát neexistuje.
Pokud však v určitém okamžiku X 0 to víme f "(x 0 ) =0, pak z toho nelze usuzovat, že v bodě X 0 funkce má extrém.
Například.
.Ale tečka X=0 není extrémní bod, protože nalevo od tohoto bodu jsou hodnoty funkcí umístěny pod osou Vůl a vpravo nahoře.
Volají se hodnoty argumentu z domény funkce, ve které derivace funkce zaniká nebo neexistuje kritické body.
Ze všeho výše uvedeného vyplývá, že extrémní body funkce patří mezi kritické body a ne každý kritický bod je však extrémním bodem. Chcete-li tedy najít extrém funkce, musíte najít všechny kritické body funkce a poté prozkoumat každý z těchto bodů samostatně na maximum a minimum. K tomuto účelu slouží následující věta.
Věta 2. (Dostačující podmínka pro existenci extrému.) Nechť je funkce spojitá na nějakém intervalu obsahujícím kritický bod X 0 a je diferencovatelný ve všech bodech tohoto intervalu (snad kromě samotného bodu X 0). Pokud při pohybu zleva doprava přes tento bod derivace změní znaménko z plus na mínus, pak v bodě X = X Funkce 0 má maximum. Pokud, při průjezdu X 0 zleva doprava, derivace změní znaménko z mínus na plus, pak má funkce v tomto bodě minimum.
Pokud tedy
f "(x)>0 at X<X 0 a f "(x)< 0 v x>x 0, tedy X 0 – maximální bod;
na X<X 0 a f "(x)> 0 v x>x 0, tedy X 0 – minimální bod.Důkaz. Předpokládejme nejprve, že při průchodu X 0 derivace mění znaménko z plus na mínus, tzn. přede všemi X, blízko k věci X 0 f "(x)> 0 pro X< x 0 , f "(x)< 0 pro x>x 0 Aplikujme na rozdíl Lagrangeovu větu f(x) - f(x 0 ) = f "(c)(x-x 0), kde C leží mezi X A X 0 .
Nechat X< x 0 Pak C< x 0 a f "(c)> 0. Proto f "(c)(x-x 0)< 0 a proto
f(x) - f(x 0 )< 0, tzn. f(x)< f(x 0 ).
Nechat x > x 0 Pak c>x 0 a f" (c)< 0. Prostředek f "(c)(x-x 0)< 0. Proto f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
Tedy pro všechny hodnoty X dost blízko X 0 f(x)< f(x 0 ) . A to znamená, že v bodě X Funkce 0 má maximum.
Druhá část věty o minimu je dokázána podobným způsobem.
Ukažme si význam této věty na obrázku. Nechat f "(x 1 ) =0 a pro všechny X, dost blízko X 1, nerovnosti jsou splněny
f "(x)< 0 v X< x 1 , f "(x)> 0 v x>x 1 .
Pak doleva od bodu X 1 se funkce zvyšuje a snižuje vpravo, tedy když X = X 1 funkce přechází z rostoucí na klesající, to znamená, že má maximum.
Podobně můžeme uvažovat o bodech X 2 a X 3 .
Vše výše uvedené lze schematicky znázornit na obrázku:
Pravidlo pro studium funkce y=f(x) pro extrém
Najděte definiční obor funkce f(x).
Najděte první derivaci funkce f "(x).
Určete pro to kritické body:
najít skutečné kořeny rovnice f "(x)=0;
najít všechny hodnoty X pro který derivát f "(x) neexistuje.
Určete znaménko derivace vlevo a vpravo od kritického bodu. Protože znaménko derivace zůstává mezi dvěma kritickými body konstantní, stačí určit znaménko derivace v jednom bodě vlevo a v jednom bodě vpravo od kritického bodu.
Vypočítejte hodnotu funkce v extrémních bodech.
Uvažujme graf spojité funkce y=f(x) znázorněno na obrázku.
Funkční hodnota v bodě X 1 bude větší než funkční hodnoty ve všech sousedních bodech jak nalevo, tak napravo X 1. V tomto případě říkáme, že funkce má v bodě X maximálně 1. Na místě X Funkce 3 má samozřejmě také maximum. Pokud vezmeme v úvahu bod X 2, pak je v něm funkční hodnota menší než všechny sousední hodnoty. V tomto případě říkáme, že funkce má v bodě X 2 minimálně. Stejně tak k věci X 4 .
Funkce y=f(x) na místě X 0 má maximum, pokud je hodnota funkce v tomto bodě větší než její hodnoty ve všech bodech nějakého intervalu obsahujícího bod X 0, tzn. pokud existuje takové okolí bodu X 0, která je pro všechny X≠X 0 , příslušnost k této čtvrti, nerovnost platí f(x)<f(x 0 ) .
Funkce y=f(x) Má to minimální na místě X 0 , pokud existuje takové okolí bodu X 0 , to je pro všechny X≠X 0 patřící do tohoto okolí, nerovnost platí f(x)>f(x 0.
Body, ve kterých funkce dosáhne svého maxima a minima, se nazývají extrémní body a hodnoty funkce v těchto bodech se nazývají extrémy funkce.
Věnujme pozornost tomu, že funkce definovaná na segmentu může dosáhnout svého maxima a minima pouze v bodech obsažených v uvažovaném segmentu.
Všimněte si, že pokud má funkce v určitém bodě maximum, neznamená to, že v tomto bodě má funkce největší hodnotu v celé definiční oblasti. Na obrázku diskutovaném výše je funkce v bodě X 1 má maximum, i když existují body, ve kterých jsou funkční hodnoty větší než v bodě X 1 . Zejména, F(X 1) < F(X 4) tj. minimum funkce je větší než maximum. Z definice maxima pouze vyplývá, že se jedná o největší hodnotu funkce v bodech dostatečně blízkých bodu maxima.
Věta 1. (Nezbytná podmínka pro existenci extrému.) Pokud je diferencovatelná funkce y=f(x) má na místě x=x 0 extrém, pak se jeho derivace v tomto bodě stane nulou.
Důkaz. Pro jistotu k bodu X Funkce 0 má maximum. Potom pro dostatečně malé přírůstky Δ X my máme f(x 0 + Δ X)
Přechod v těchto nerovnostech do limitu v Δ X→ 0 a vezmeme-li v úvahu, že derivace F "(X 0) existuje, a proto limita vlevo nezávisí na tom, jak Δ X→ 0, dostaneme: při Δ X → 0 – 0 F"(X 0) ≥ 0 a při A X → 0 + 0 F"(X 0) ≤ 0. Od F"(X 0) definuje číslo, pak jsou tyto dvě nerovnosti kompatibilní pouze tehdy, když F"(X 0) = 0.
Osvědčený teorém říká, že maximální a minimální body mohou být pouze mezi těmi hodnotami argumentu, při kterých se derivace stává nulou.
Uvažovali jsme případ, kdy funkce má derivaci ve všech bodech určitého segmentu. Jaká je situace v případech, kdy derivát neexistuje? Podívejme se na příklady.
Příklady.
- y=|X|.
Funkce nemá v bodě derivaci X=0 (v tomto bodě nemá graf funkce definovanou tečnu), ale v tomto bodě má funkce minimum, protože y(0)=0 a pro všechny X≠ 0y > 0.
- Nechat X< x
0 Pak C< x
0 a f "(c)> 0.
Proto f "(c)(x-x 0)<
0 a proto
f(x) - f(x 0 )< 0, tzn. f(x)< f(x 0 ).
- Nechat x > x 0 Pak c>x 0 a f" (c)< 0. Prostředek f "(c)(x-x 0)< 0. Proto f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Najděte definiční obor funkce f(x).
- Najděte první derivaci funkce f "(x).
- Určete pro to kritické body:
- najít skutečné kořeny rovnice f "(x)=0;
- najít všechny hodnoty X pro který derivát f "(x) neexistuje.
- Určete znaménko derivace vlevo a vpravo od kritického bodu. Protože znaménko derivace zůstává mezi dvěma kritickými body konstantní, stačí určit znaménko derivace v jednom bodě vlevo a v jednom bodě vpravo od kritického bodu.
- Vypočítejte hodnotu funkce v extrémních bodech.
- Najděte všechny kritické body funkce v intervalu ( a, b) a vypočítat hodnoty funkce v těchto bodech.
- Vypočítejte hodnoty funkce na koncích segmentu, když x = a, x = b.
- Ze všech získaných hodnot vyberte největší a nejmenší.
Funkce nemá derivaci at X=0, protože to jde do nekonečna X=0. Ale v tomto okamžiku má funkce maximum.

Funkce nemá derivaci at X=0, protože ![]() na X→0. V tomto bodě funkce nemá ani maximum, ani minimum. Opravdu, f(x)=0 a při X<0f(x)<0, а при X>0f(x)>0.
na X→0. V tomto bodě funkce nemá ani maximum, ani minimum. Opravdu, f(x)=0 a při X<0f(x)<0, а при X>0f(x)>0.

Z uvedených příkladů a formulované věty je tedy zřejmé, že funkce může mít extrém pouze ve dvou případech: 1) v bodech, kde derivace existuje a je rovna nule; 2) v bodě, kde derivát neexistuje.
Pokud však v určitém okamžiku X 0 to víme f "(x 0 ) =0, pak z toho nelze usuzovat, že v bodě X 0 funkce má extrém.
Například. ![]() .
.

Ale tečka X=0 není extrémní bod, protože nalevo od tohoto bodu jsou hodnoty funkcí umístěny pod osou Vůl a vpravo nahoře.
Volají se hodnoty argumentu z domény funkce, ve které derivace funkce zaniká nebo neexistuje kritické body.
Ze všeho výše uvedeného vyplývá, že extrémní body funkce patří mezi kritické body a ne každý kritický bod je však extrémním bodem. Chcete-li tedy najít extrém funkce, musíte najít všechny kritické body funkce a poté prozkoumat každý z těchto bodů samostatně na maximum a minimum. K tomuto účelu slouží následující věta.
Věta 2. (Dostatečná podmínka pro existenci extrému.) Nechť je funkce spojitá na nějakém intervalu obsahujícím kritický bod X 0 a je diferencovatelný ve všech bodech tohoto intervalu (snad kromě samotného bodu X 0). Pokud při pohybu zleva doprava přes tento bod derivace změní znaménko z plus na mínus, pak v bodě X = X Funkce 0 má maximum. Pokud, při průjezdu X 0 zleva doprava, derivace změní znaménko z mínus na plus, pak má funkce v tomto bodě minimum.
Pokud tedy
Důkaz. Předpokládejme nejprve, že při průchodu X 0 derivace mění znaménko z plus na mínus, tzn. přede všemi X, blízko k věci X 0 f "(x)> 0 pro X< x 0 , f "(x)< 0 pro x>x 0 Aplikujme na rozdíl Lagrangeovu větu f(x) - f(x 0 ) = f "(c)(x-x 0), kde C leží mezi X A X 0 .
Tedy pro všechny hodnoty X dost blízko X 0 f(x)< f(x 0 ) . A to znamená, že v bodě X Funkce 0 má maximum.
Druhá část věty o minimu je dokázána podobným způsobem.

Ukažme si význam této věty na obrázku. Nechat f "(x 1 ) =0 a pro všechny X, dost blízko X 1, nerovnosti jsou splněny
f "(x)< 0 v X< x 1 , f "(x)> 0 v x>x 1 .
Pak doleva od bodu X 1 se funkce zvyšuje a snižuje vpravo, tedy když X = X 1 funkce přechází z rostoucí na klesající, to znamená, že má maximum.
Podobně můžeme uvažovat o bodech X 2 a X 3 .

Vše výše uvedené lze schematicky znázornit na obrázku:
Pravidlo pro studium funkce y=f(x) pro extrém
Příklady. Prozkoumejte funkce pro minimum a maximum.
MAXIMÁLNÍ A NEJMENŠÍ HODNOTY FUNKCE NA Segmentu
Největší hodnota funkce na intervalu je největší ze všech jejích hodnot na tomto intervalu a nejmenší– nejmenší ze všech svých hodnot.
Zvažte funkci y=f(x) spojitý na segmentu [ a, b]. Jak známo, taková funkce dosahuje svých maximálních a minimálních hodnot buď na hranici segmentu, nebo uvnitř něj. Pokud je největší nebo nejmenší hodnota funkce dosažena ve vnitřním bodě segmentu, pak je tato hodnota maximem nebo minimem funkce, to znamená, že je dosažena v kritických bodech.
Dostáváme tedy následující pravidlo pro nalezení největší a nejmenší hodnoty funkce na segmentu[ a, b] :
Nechť je funkce $z=f(x,y)$ definována v nějakém okolí bodu $(x_0,y_0)$. Říkají, že $(x_0,y_0)$ je (místní) maximální bod, pokud pro všechny body $(x,y)$ v nějakém okolí bodu $(x_0,y_0)$ je nerovnost $f(x,y) je spokojen< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, pak se bod $(x_0,y_0)$ nazývá (místní) minimální bod.
Maximální a minimální body jsou často nazývány obecným pojmem - extrémní body.
Je-li $(x_0,y_0)$ maximální bod, pak hodnota funkce $f(x_0,y_0)$ v tomto bodě se nazývá maximum funkce $z=f(x,y)$. Podle toho se hodnota funkce v bodě minima nazývá minimum funkce $z=f(x,y)$. Minima a maxima funkce jsou spojena společným pojmem - extrémy funkce.
Algoritmus pro studium funkce $z=f(x,y)$ pro extrém
- Najděte parciální derivace $\frac(\partial z)(\partial x)$ a $\frac(\partial z)(\partial y)$. Sestavte a vyřešte soustavu rovnic $ \left \( \begin(zarovnáno) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 \ end(zarovnáno) \right.$ Body, jejichž souřadnice splňují zadaný systém, se nazývají stacionární.
- Najít $\frac(\partial^2z)(\částečné x^2)$, $\frac(\částečné^2z)(\částečné x\částečné y)$, $\frac(\částečné^2z)(\částečné y^2)$ a vypočítejte hodnotu $\Delta=\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ v každém stacionárním bodě. Poté použijte následující schéma:
- Pokud $\Delta > 0$ a $\frac(\partial^2z)(\partial x^2) > 0$ (nebo $\frac(\partial^2z)(\partial y^2) > 0$), pak je bod, který je předmětem studia, minimální bod.
- Pokud $\Delta > 0$ a $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Pokud $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
- Jestliže $\Delta = 0$, pak nelze o přítomnosti extrému říci nic určitého; je nutný další výzkum.
Poznámka (žádoucí pro úplnější porozumění textu): show\hide
Pokud $\Delta > 0$, pak $\frac(\partial^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2)-\left(\frac(\ částečné^2z)(\částečné x\částečné y) \vpravo)^2 > 0$. A z toho plyne, že $\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2) > \left(\frac(\částečné^2z) ( \částečné x\částečné y)\vpravo)^2 ≥ 0$. Tito. $\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2) > 0$. Pokud je součin určitých veličin větší než nula, pak jsou tyto veličiny stejného znaménka. To je například, pokud $\frac(\partial^2z)(\částečné x^2) > 0$, pak $\frac(\částečné^2z)(\částečné y^2) > 0$. Stručně řečeno, pokud $\Delta > 0$, pak se znaménka $\frac(\partial^2z)(\partial x^2)$ a $\frac(\partial^2z)(\partial y^2)$ shodují .
Příklad č. 1
Prozkoumejte funkci $z=4x^2-6xy-34x+5y^2+42y+7$ pro její extrém.
$$ \frac(\částečné z)(\částečné x)=8x-6y-34; \frac(\částečné z)(\částečné y)=-6x+10y+42. $$
$$ \left \( \začátek(zarovnáno) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(zarovnáno) \vpravo. $$
Zmenšíme každou rovnici tohoto systému o $2$ a přesuneme čísla na pravou stranu rovnic:
$$ \left \( \začátek(zarovnáno) & 4x-3y=17;\\ & -3x+5y=-21. \end(zarovnáno) \vpravo. $$
Získali jsme soustavu lineárních algebraických rovnic. V této situaci se mi zdá nejvhodnější použít k řešení výsledného systému Cramerovu metodu.
$$ \begin(zarovnáno) & \Delta=\left| \begin(pole) (cc) 4 & -3\\ -3 & 5 \end(pole)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\left| \begin(pole) (cc) 17 & -3\\ -21 & 5 \end(pole)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\left| \begin(pole) (cc) 4 & 17\\ -3 & -21 \end(pole)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(zarovnáno) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$
Hodnoty $x=2$, $y=-3$ jsou souřadnicemi stacionárního bodu $(2;-3)$.
$$ \frac(\částečné^2 z)(\částečné x^2)=8; \frac(\částečné^2 z)(\částečné y^2)=10; \frac(\částečné^2 z)(\částečné x \částečné y)=-6. $$
Vypočítejme hodnotu $\Delta$:
$$ \Delta=\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2)-\left(\frac(\částečné^2z)( \částečné x\částečné y) \vpravo)^2= 8\cdot 10-(-6)^2=80-36=44. $$
Protože $\Delta > 0$ a $\frac(\partial^2 z)(\partial x^2) > 0$, pak podle bodu $(2;-3)$ je minimální bod funkce $ z$. Minimum funkce $z$ najdeme dosazením souřadnic bodu $(2;-3)$ do dané funkce:
$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$
Odpovědět: $(2;-3)$ - minimální bod; $z_(min)=-90$.
Příklad č. 2
Prozkoumejte funkci $z=x^3+3xy^2-15x-12y+1$ pro její extrém.
Budeme se řídit výše uvedeným. Nejprve najdeme parciální derivace prvního řádu:
$$ \frac(\částečné z)(\částečné x)=3x^2+3y^2-15; \frac(\částečné z)(\částečné y)=6xy-12. $$
Vytvořme soustavu rovnic $ \left \( \begin(zarovnáno) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( zarovnáno) \right.$:
$$ \left \( \začátek(zarovnáno) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(zarovnáno) \vpravo. $$
Zmenšíme první rovnici o 3 a druhou o 6.
$$ \left \( \začátek(zarovnáno) & x^2+y^2-5=0;\\ & xy-2=0. \end(zarovnáno) \vpravo. $$
Pokud $x=0$, pak nás druhá rovnice přivede k rozporu: $0\cdot y-2=0$, $-2=0$. Proto závěr: $x\neq 0$. Pak z druhé rovnice máme: $xy=2$, $y=\frac(2)(x)$. Dosazením $y=\frac(2)(x)$ do první rovnice získáme:
$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$
Máme bikvadratickou rovnici. Provedeme náhradu $t=x^2$ (což znamená, že $t > 0$):
$$ t^2-5t+4=0;\\ \begin(zarovnáno) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(zarovnáno) $$
Pokud $t=1$, pak $x^2=1$. Máme tedy dvě hodnoty $x$: $x_1=1$, $x_2=-1$. Pokud $t=4$, pak $x^2=4$, tzn. $x_3=2$, $x_4=-2$. Když si zapamatujeme, že $y=\frac(2)(x)$, dostaneme:
\begin(zarovnáno) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2) = -1. \end (zarovnáno)
Máme tedy čtyři stacionární body: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Tím je dokončen první krok algoritmu.
Nyní začněme s algoritmem. Pojďme najít parciální derivace druhého řádu:
$$ \frac(\částečné^2 z)(\částečné x^2)=6x; \frac(\částečné^2 z)(\částečné y^2)=6x; \frac(\částečné^2 z)(\částečné x \částečné y)=6y. $$
Pojďme najít $\Delta$:
$$ \Delta=\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2)-\left(\frac(\částečné^2z)( \částečné x\částečné y) \vpravo)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$
Nyní vypočítáme hodnotu $\Delta$ v každém z dříve nalezených stacionárních bodů. Začněme od bodu $M_1(1;2)$. V tomto okamžiku máme: $\Delta(M_1)=36(1^2-2^2)=-108$. Od $\Delta (M_1)< 0$, то согласно в точке $M_1$ экстремума нет.
Prozkoumejme bod $M_2(-1;-2)$. V tomto okamžiku máme: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Od $\Delta (M_2)< 0$, то согласно в точке $M_2$ экстремума нет.
Prozkoumejme bod $M_3(2;1)$. V tomto bodě dostáváme:
$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\částečné^2 z)(\částečné x^2)\pravé|_(M_3)=6\cdot 2=12. $$
Protože $\Delta(M_3) > 0$ a $\left.\frac(\částečné^2 z)(\částečné x^2)\pravé|_(M_3) > 0$, pak podle $M_3(2; 1)$ je minimální bod funkce $z$. Minimum funkce $z$ najdeme dosazením souřadnic bodu $M_3$ do dané funkce:
$$ z_(min)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$
Zbývá prozkoumat bod $M_4(-2;-1)$. V tomto bodě dostáváme:
$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\částečné^2 z)(\částečné x^2)\pravé|_(M_4)=6\cdot (-2)=-12. $$
Protože $\Delta(M_4) > 0$ a $\left.\frac(\částečné^2 z)(\částečné x^2)\vpravo|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$
Extrémní studie je dokončena. Nezbývá než zapsat odpověď.
Odpovědět:
- $(2;1)$ - minimální bod, $z_(min)=-27$;
- $(-2;-1)$ - maximální bod, $z_(max)=29$.
Poznámka
V obecném případě není potřeba počítat hodnotu $\Delta$, protože nás zajímá pouze znaménko, nikoli konkrétní hodnota tohoto parametru. Například, například č. 2 uvažované výše, v bodě $M_3(2;1)$ máme $\Delta=36\cdot(2^2-1^2)$. Zde je zřejmé, že $\Delta > 0$ (protože oba faktory $36$ a $(2^2-1^2)$ jsou kladné) a není možné najít konkrétní hodnotu $\Delta$. Je pravda, že pro standardní výpočty je tato poznámka zbytečná - tam vyžadují, abyste výpočty uvedli na číslo :)
Příklad č. 3
Prozkoumejte funkci $z=x^4+y^4-2x^2+4xy-2y^2+3$ pro její extrém.
Budeme následovat. Nejprve najdeme parciální derivace prvního řádu:
$$ \frac(\částečné z)(\částečné x)=4x^3-4x+4y; \frac(\částečné z)(\částečné y)=4y^3+4x-4y. $$
Vytvořme soustavu rovnic $ \left \( \begin(zarovnáno) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( zarovnáno) \right.$:
$$ \left \( \begin(zarovnáno) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(zarovnáno) \vpravo. $$
Snižme obě rovnice o 4 $:
$$ \left \( \začátek(zarovnáno) & x^3-x+y=0;\\ & y^3+x-y=0. \end(zarovnáno) \vpravo. $$
Přidejme první rovnici k druhé a vyjádřime $y$ v podmínkách $x$:
$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$
Dosazením $y=-x$ do první rovnice systému získáme:
$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$
Z výsledné rovnice máme: $x=0$ nebo $x^2-2=0$. Z rovnice $x^2-2=0$ vyplývá, že $x=-\sqrt(2)$ nebo $x=\sqrt(2)$. Takže byly nalezeny tři hodnoty $x$, konkrétně: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Protože $y=-x$, pak $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.
První krok řešení je dokončen. Máme tři stacionární body: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .
Nyní začněme s algoritmem. Pojďme najít parciální derivace druhého řádu:
$$ \frac(\částečné^2 z)(\částečné x^2)=12x^2-4; \frac(\částečné^2 z)(\částečné y^2)=12y^2-4; \frac(\částečné^2 z)(\částečné x \částečné y)=4. $$
Pojďme najít $\Delta$:
$$ \Delta=\frac(\částečné^2z)(\částečné x^2)\cdot \frac(\částečné^2z)(\částečné y^2)-\left(\frac(\částečné^2z)( \částečné x\částečné y) \vpravo)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$
Nyní vypočítáme hodnotu $\Delta$ v každém z dříve nalezených stacionárních bodů. Začněme od bodu $M_1(0;0)$. V tomto okamžiku máme: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Protože $\Delta(M_1) = 0$, je zapotřebí další výzkum, protože o přítomnosti extrému v uvažovaném bodě nelze říci nic určitého. Nechme tento bod prozatím na pokoji a přejděme k dalším bodům.
Prozkoumejme bod $M_2(-\sqrt(2),\sqrt(2))$. V tomto bodě dostáváme:
\begin(zarovnáno) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end (zarovnáno)
Protože $\Delta(M_2) > 0$ a $\left.\frac(\částečné^2 z)(\částečné x^2)\pravé|_(M_2) > 0$, pak podle $M_2(-\ sqrt(2),\sqrt(2))$ je minimální bod funkce $z$. Minimum funkce $z$ najdeme dosazením souřadnic bodu $M_2$ do dané funkce:
$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$
Podobně jako v předchozím bodě zkoumáme bod $M_3(\sqrt(2),-\sqrt(2))$. V tomto bodě dostáváme:
\begin(zarovnáno) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end (zarovnáno)
Protože $\Delta(M_3) > 0$ a $\left.\frac(\částečné^2 z)(\částečné x^2)\pravé|_(M_3) > 0$, pak podle $M_3(\sqrt (2),-\sqrt(2))$ je minimální bod funkce $z$. Minimum funkce $z$ najdeme dosazením souřadnic bodu $M_3$ do dané funkce:
$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2) ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$
Je čas vrátit se k bodu $M_1(0;0)$, ve kterém $\Delta(M_1) = 0$. Podle toho je zapotřebí další výzkum. Tato vyhýbavá fráze znamená „dělejte si, co chcete“ :). Neexistuje obecný způsob, jak takové situace řešit, a to je pochopitelné. Pokud by taková metoda existovala, byla by již dávno obsažena ve všech učebnicích. Mezitím musíme hledat speciální přístup ke každému bodu, ve kterém $\Delta = 0$. Nuže, prozkoumejme chování funkce v okolí bodu $M_1(0;0)$. Okamžitě si všimněme, že $z(M_1)=z(0;0)=3$. Předpokládejme, že $M_1(0;0)$ je minimální bod. Pak pro libovolný bod $M$ z nějakého okolí bodu $M_1(0;0)$ získáme $z(M) > z(M_1)$, tzn. $z(M) > 3$. Co když nějaká čtvrť obsahuje body, při kterých $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Uvažujme body, pro které $y=0$, tj. body ve tvaru $(x,0)$. V těchto bodech bude funkce $z$ nabývat následujících hodnot:
$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$
Ve všech dostatečně malých čtvrtích $M_1(0;0)$ máme $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Ale možná je bod $M_1(0;0)$ maximální bod? Pokud je tomu tak, pak pro libovolný bod $M$ z nějakého okolí bodu $M_1(0;0)$ získáme $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3 $? Pak určitě nebude v bodě $M_1$ žádné maximum.
Uvažujme body, pro které $y=x$, tzn. body ve tvaru $(x,x)$. V těchto bodech bude funkce $z$ nabývat následujících hodnot:
$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$
Protože v libovolném okolí bodu $M_1(0;0)$ máme $2x^4 > 0$, pak $2x^4+3 > 3$. Závěr: libovolné okolí bodu $M_1(0;0)$ obsahuje body, ve kterých $z > 3$, proto bod $M_1(0;0)$ nemůže být maximálním bodem.
Bod $M_1(0;0)$ není maximální ani minimální bod. Závěr: $M_1$ není vůbec extrémní bod.
Odpovědět: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ jsou minimální body funkce $z$. V obou bodech $z_(min)=-5$.
Bod x 0 se nazývá maximální bod(minimální) funkce f(x), je-li v některém okolí bodu x 0 splněna nerovnost f(x) ≤f(x 0) (f(x) ≥f(x 0)).
Hodnota funkce v tomto bodě se nazývá odpovídajícím způsobem maximum nebo minimální funkcí. Maximální a minimální funkce jsou spojeny společným názvem extrém funkcí.
Extrém funkce v tomto smyslu se často nazývá lokální extrém, zdůrazňující skutečnost, že tento pojem je spojen pouze s dostatečně malým okolím bodu x 0. Na stejném intervalu může mít funkce několik lokálních maxim a minim, která se nemusí nutně shodovat globální maximum nebo minimální(tj. největší nebo nejmenší hodnota funkce za celý interval).
Nutná podmínka pro extrém. Aby funkce měla v bodě extrém, je nutné, aby její derivace v tomto bodě byla rovna nule nebo neexistovala.
U diferencovatelných funkcí tato podmínka vyplývá z Fermatovy věty. Kromě toho také počítá s případem, kdy má funkce extrém v bodě, ve kterém není diferencovatelná.
Volají se body, ve kterých je splněna nezbytná extrémní podmínka kritický(nebo stacionární pro diferencovatelnou funkci). Tyto body musí být v rámci domény funkce.
Pokud je tedy v kterémkoli bodě extrém, pak je tento bod kritický (nezbytná podmínka). Všimněte si, že opak není pravdou. Kritický bod nemusí být nutně extrémním bodem, tj. uvedená podmínka není dostatečná.
První postačující podmínka pro extrém. Pokud při průchodu určitým bodem derivace diferencovatelné funkce změní své znaménko z plus na mínus, pak je to maximální bod funkce, a pokud z mínus do plus, pak je to minimální bod.
Důkaz této podmínky vyplývá z postačující podmínky monotonie (při změně znaménka derivace dochází buď k přechodu z nárůstu funkce na pokles, nebo z poklesu na nárůst).
Druhá postačující podmínka pro extrém. Jestliže první derivace dvakrát diferencovatelné funkce v nějakém bodě je nula a druhá derivace v tomto bodě je kladná, pak je to minimální bod funkce; a pokud je druhá derivace záporná, pak je to maximální bod.
Důkaz tohoto stavu je založen i na dostatečné podmínce monotónnosti. Ve skutečnosti, pokud je druhá derivace kladná, pak je první derivace rostoucí funkcí. Protože se v daném bodě rovná nule, při průchodu jím změní znaménko z mínus na plus, čímž se vrátíme k první dostatečné podmínce pro lokální minimum. Podobně, pokud je druhá derivace záporná, pak první klesá a mění znaménko z plus na mínus, což je dostatečná podmínka pro lokální maximum.
Studium funkce pro extrém v souladu s formulovanými teorémy zahrnuje následující fáze:
1. Najděte první derivaci funkce f`(x).
2. Zkontrolujte splnění nezbytné extrémní podmínky, tzn. najděte kritické body funkce f(x), ve kterých derivace f`(x) = 0 nebo neexistuje.
3. Zkontrolujte splnění postačující podmínky pro extrém, tzn. buď prozkoumejte znaménko derivace vlevo a vpravo od každého kritického bodu, nebo najděte druhou derivaci f``(x) a určete její znaménko v každém kritickém bodě. Udělejte závěr o přítomnosti extrémů funkce.
4. Najděte extrémy (extrémní hodnoty) funkce.
Hledání globálního maxima a minima funkce po určitou dobu má i velký praktický význam. Řešení tohoto problému na segmentu je založeno na Weierstrassově teorému, podle kterého spojitá funkce nabývá na segmentu své největší a nejmenší hodnoty. Lze jich dosáhnout jak v extrémních bodech, tak na koncích segmentu. Řešení proto zahrnuje následující kroky:
1. Najděte derivaci funkce f`(x).
2. Najděte kritické body funkce f(x), ve kterých derivace f`(x) = 0 nebo neexistuje.
3. Najděte hodnoty funkce v kritických bodech a na koncích segmentu a vyberte z nich největší a nejmenší.
Jedná se o poměrně zajímavý úsek matematiky, se kterým se setkávají naprosto všichni absolventi a studenti. Ne každému se však matan líbí. Někteří nedokážou pochopit ani základní věci, jako je zdánlivě standardní funkční studie. Tento článek je určen k nápravě takového nedopatření. Chcete se dozvědět více o funkční analýze? Chtěli byste vědět, co jsou extrémní body a jak je najít? Pak je tento článek právě pro vás.
Studium grafu funkce
Za prvé, stojí za to pochopit, proč vůbec potřebujete analyzovat graf. Existují jednoduché funkce, které není těžké nakreslit. Pozoruhodným příkladem takové funkce je parabola. Nakreslit graf nebude těžké. Stačí pomocí jednoduché transformace najít čísla, ve kterých funkce nabývá hodnoty 0. A to je v zásadě vše, co potřebujete vědět, abyste mohli nakreslit graf paraboly.
Ale co když je funkce, kterou potřebujeme vykreslit, mnohem složitější? Protože vlastnosti komplexních funkcí nejsou zcela zřejmé, je nutné provést celou analýzu. Teprve poté lze funkci znázornit graficky. Jak to udělat? Odpověď na tuto otázku najdete v tomto článku.
Plán funkční analýzy
První věc, kterou musíme udělat, je provést povrchní studii funkce, během níž najdeme doménu definice. Začněme tedy popořadě. Definiční doména je množina hodnot, kterými je funkce definována. Jednoduše řečeno, jde o čísla, která lze použít ve funkci místo x. Pro určení rozsahu se stačí podívat do záznamu. Například je zřejmé, že funkce y (x) = x 3 + x 2 - x + 43 má definiční obor, kterým je množina reálných čísel. No, s funkcí jako (x 2 - 2x)/x je všechno trochu jinak. Protože číslo ve jmenovateli se nesmí rovnat 0, definičním oborem této funkce budou všechna reálná čísla jiná než nula.
Dále je potřeba najít tzv. nuly funkce. Toto jsou hodnoty argumentů, při kterých má celá funkce hodnotu nula. K tomu je nutné funkci přirovnat k nule, podrobně ji zvážit a provést některé transformace. Vezměme si již známou funkci y(x) = (x 2 - 2x)/x. Ze školního kurzu víme, že zlomek je roven 0, když je čitatel roven nule. Proto jmenovatele zahodíme a začneme pracovat s čitatelem, který se rovná nule. Dostaneme x 2 - 2x = 0 a vyjmeme x ze závorek. Proto x (x - 2) = 0. Ve výsledku zjistíme, že naše funkce je rovna nule, když se x rovná 0 nebo 2.
Při zkoumání grafu funkce se mnoho lidí setkává s problémy v podobě extrémních bodů. A je to zvláštní. Koneckonců, extrémy jsou docela jednoduché téma. nevěříš mi? Přesvědčte se sami přečtením této části článku, ve které budeme hovořit o minimálních a maximálních bodech.

Za prvé, stojí za to pochopit, co je extrém. Extrém je mezní hodnota, které funkce dosáhne v grafu. Ukazuje se, že existují dvě extrémní hodnoty - maximální a minimální. Pro názornost se můžete podívat na obrázek výše. Ve studované oblasti je bod -1 maximem funkce y (x) = x 5 - 5x a bod 1 je tedy minimem.
Nepleťte si také pojmy. Extrémní body funkce jsou ty argumenty, ve kterých daná funkce nabývá extrémních hodnot. Extrémem je zase hodnota minima a maxima funkce. Zvažte například znovu obrázek výše. -1 a 1 jsou extrémní body funkce a 4 a -4 jsou samotné extrémy.
Hledání extrémních bodů

Ale jak najdete extrémní body funkce? Všechno je docela jednoduché. První věc, kterou musíte udělat, je najít derivaci rovnice. Řekněme, že jsme dostali úkol: „Najděte extrémní body funkce y (x), argument je x. Pro názornost vezměme funkci y (x) = x 3 + 2x 2 + x + 54. získáme následující rovnici: 3x 2 + 4x + 1. Výsledkem je standardní kvadratická rovnice. Vše, co musíme udělat, je přirovnat ji k nule a najít kořeny. Protože diskriminant je větší než nula (D = 16 - 12 = 4), tato rovnice je určena dvěma kořeny. Najděte je a získejte dvě hodnoty: 1/3 a -1. To budou extrémní body funkce. Jak však můžete stále určit, kdo je kdo? Který bod je maximum a který minimum? Chcete-li to provést, musíte vzít sousední bod a zjistit jeho hodnotu. Například vezměte číslo -2, které se nachází vlevo podél souřadnicové čáry od -1 Tuto hodnotu dosaďte do naší rovnice y(-2) = 12 - 8 + 1 = 5. Výsledkem je kladné číslo, což znamená, že v intervalu od Funkce vzroste z 1/3 na -1. , zase znamená, že na intervalech od mínus nekonečna do 1/3 a od -1 do plus nekonečna funkce klesá. Můžeme tedy uzavřít, že číslo 1/3 je minimální bod funkce na studovaném intervalu a -1 je maximální bod.

Za zmínku také stojí, že jednotná státní zkouška vyžaduje nejen nalezení extrémních bodů, ale také provedení nějaké operace s nimi (sčítání, násobení atd.). Z tohoto důvodu stojí za to věnovat zvláštní pozornost podmínkám problému. Nepozorností totiž můžete přijít o body.




