Keresse meg és fedezze fel a függvény szélsőpontjait. A függvény szélsőértékének második jele

Bevezetés

A tudomány számos területén és a gyakorlati tevékenységek során gyakran meg kell küzdeni a függvény szélsőértékének megtalálásának problémájával. Az tény, hogy számos műszaki, gazdasági stb. A folyamatokat egy vagy több függvény modellezi, amelyek változóktól – a modellezett jelenség állapotát befolyásoló tényezőktől – függenek. Az optimális (racionális) állapot és folyamatszabályozás meghatározásához meg kell találni az ilyen függvények szélsőértékeit. Tehát a közgazdaságtanban gyakran megoldódnak a költségek minimalizálásának vagy a profit maximalizálásának problémái - ez a vállalat mikroökonómiai problémája. Ebben a munkában nem foglalkozunk modellezési kérdésekkel, hanem csak a függvények szélsőségeinek keresési algoritmusait vesszük figyelembe a legegyszerűbb változatban, amikor a változókra nincs korlátozva (feltétel nélküli optimalizálás), és az extrémumot csak egy célfüggvényre keressük.

A FUNKCIÓ EXTRÉMÁJA

Tekintsük egy folytonos függvény grafikonját y=f(x)ábrán látható. Funkció értéke egy pontban x 1 nagyobb lesz, mint a függvényértékek az összes szomszédos pontban, mind balra, mind jobbra x 1 . Ebben az esetben azt mondjuk, hogy a függvénynek a pontja van x 1 maximum. Azon a ponton x A 3. függvénynek nyilván van maximuma is. Ha figyelembe vesszük a lényeget x 2, akkor a benne lévő függvény értéke kisebb, mint az összes szomszédos érték. Ebben az esetben azt mondjuk, hogy a függvénynek a pontja van x 2 minimum. Hasonlóan a lényeghez x 4 .

Funkció y=f(x) azon a ponton x 0 rendelkezik maximális, ha a függvény értéke ezen a ponton nagyobb, mint a pontot tartalmazó intervallum összes pontjában elért értékei x 0, azaz ha van egy pontnak ilyen környéke x 0, ami mindenkinek szól x≠x 0 , ehhez a szomszédsághoz tartozik az egyenlőtlenség f(x)<f(x 0 ) .

Funkció y=f(x) Megvan minimális azon a ponton x 0 , ha van egy pontnak ilyen környéke x 0 , ez mindenkinek szól x≠x 0 ehhez a szomszédsághoz tartozó egyenlőtlenség fennáll f(x)>f(x 0.

Azokat a pontokat, ahol a függvény eléri maximumát és minimumát, szélsőséges pontoknak nevezzük, a függvény értékeit pedig ezekben a pontokban a függvény szélsőértékeinek.

Figyeljünk arra, hogy egy szakaszon definiált függvény csak a vizsgált szakaszon belüli pontokban érheti el maximumát és minimumát.

Vegye figyelembe, hogy ha egy függvénynek egy pontban van maximuma, ez nem jelenti azt, hogy azon a ponton a függvénynek a legnagyobb értéke van a teljes definíciós tartományban. A fent tárgyalt ábrán a pontban lévő függvény x 1-nek van maximuma, bár vannak olyan pontok, ahol a függvényértékek nagyobbak, mint a ponton x 1 . Különösen, f(x 1) < f(x 4) azaz. egy függvény minimuma nagyobb, mint a maximum. A maximum definíciójából csak az következik, hogy ez a függvény legnagyobb értéke a maximum ponthoz kellően közeli pontokban.

1. Tétel (A szélsőség létezésének szükséges feltétele.) Ha a differenciálható függvény y=f(x) pontban van x= x 0 extrémum, akkor a deriváltja ezen a ponton nulla lesz.

Bizonyíték. Hagyjuk, a határozottság kedvéért a pontnál x A 0 függvénynek maximuma van. Ekkor kellően kis lépésekben Δ x nekünk van f(x 0 + Δ x) 0 ) , azaz

De aztán
Ezeket az egyenlőtlenségeket átengedjük a Δ-nél lévő határértékre x→ 0 és figyelembe véve, hogy a derivált f "(x 0) létezik, ezért a bal oldali határérték nem függ attól, hogyan Δ x→ 0, kapjuk: Δ-nél x → 0 – 0 f"(x 0) ≥ 0 a Δ-nél x → 0 + 0 f"(x 0) ≤ 0. Mivel f"(x 0) definiál egy számot, akkor ez a két egyenlőtlenség csak akkor kompatibilis, ha f"(x 0) = 0.

A bizonyított tétel kimondja, hogy a maximum és minimum pont csak az argumentum azon értékei között lehet, amelyeknél a derivált nullává válik.

Azt az esetet vizsgáltuk, amikor egy függvénynek egy adott szegmens minden pontján deriváltja van. Mi a helyzet azokban az esetekben, amikor a derivatíva nem létezik? Nézzünk példákat.

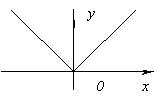
y=|x|.

A függvénynek nincs deriváltja a ponton x=0 (ezen a ponton a függvény grafikonjának nincs definiált érintője), de ezen a ponton a függvénynek van minimuma, mivel y(0)=0, és mindenre x≠ 0y > 0.
nincs származéka at x=0, mivel a végtelenbe megy x=0. De ezen a ponton a függvénynek van maximuma. nincs származéka at x=0, mióta x→0. Ezen a ponton a függvénynek nincs sem maximuma, sem minimuma. Igazán, f(x)=0 és at x<0f(x)<0, а при x>0f(x)>0.
A megadott példákból és a megfogalmazott tételből tehát világos, hogy egy függvénynek csak két esetben lehet szélsőértéke: 1) azokon a pontokon, ahol a derivált létezik és egyenlő nullával; 2) azon a ponton, ahol a származék nem létezik.

Ha azonban valamikor x 0 ezt tudjuk f "(x 0 ) =0, akkor ebből nem lehet arra következtetni, hogy azon a ponton x 0 a függvénynek szélsőértéke van.

Például.
.
De időszak x A =0 nem szélsőpont, mivel ettől a ponttól balra a függvényértékek a tengely alatt találhatók Ökör, és jobbra fent.

Egy függvény tartományából származó argumentum értékeit, ahol a függvény deriváltja eltűnik vagy nem létezik, nevezzük. kritikus pontok.

A fentiekből következik, hogy a függvény szélsőpontjai a kritikus pontok közé tartoznak, de nem minden kritikus pont szélsőpont. Ezért egy függvény szélsőértékének megtalálásához meg kell találni a függvény összes kritikus pontját, majd ezeket a pontokat külön-külön meg kell vizsgálni a maximum és a minimum szempontjából. Ezt a célt szolgálja a következő tétel.

2. Tétel (Elegendő feltétele a szélsőség létezésének.) Legyen a függvény folytonos valamely kritikus pontot tartalmazó intervallumon x 0, és ennek az intervallumnak minden pontján differenciálható (kivéve talán magát a pontot x 0). Ha ezen a ponton balról jobbra haladva a derivált előjelet vált pluszról mínuszra, akkor a pontban x = x A 0 függvénynek maximuma van. Ha áthaladáskor x 0 balról jobbra, a derivált mínuszról pluszra változtatja az előjelet, ekkor a függvénynek ezen a ponton van minimuma.

Így ha

f "(x)>0 at x<x 0 és f "(x)< 0 órakor x> x 0, akkor x 0 – maximális pont;
nál nél x<x 0 és f "(x)> 0 órakor x> x 0, akkor x 0 – minimum pont.
Bizonyíték. Először tegyük fel, hogy amikor áthaladunk x 0 a derivált az előjelet pluszról mínuszra változtatja, azaz. mindenki előtt x, közel a lényeghez x 0 f "(x)> 0 érte x< x 0 , f "(x)< 0 érte x> x 0 . Alkalmazzuk Lagrange tételét a különbségre f(x) - f(x 0 ) = f "(c)(x-x 0), hol c között fekszik xÉs x 0 .

Hadd x< x 0 . Akkor c< x 0 és f "c)> 0. Ezért f "(c)(x-x 0)< 0 és ezért

f(x) - f(x 0 )< 0, azaz f(x)< f(x 0 ).

Hadd x > x 0 . Akkor c>x 0 és f "(c)< 0. Eszközök f "(c)(x-x 0)< 0. Ezért f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Így minden értékre x elég közel ahhoz x 0 f(x)< f(x 0 ) . Ez pedig azt jelenti, hogy pont x A 0 függvénynek maximuma van.

A minimumtétel második részét hasonló módon bizonyítjuk.

Illusztráljuk ennek a tételnek a jelentését az ábrán. Hadd f "(x 1 ) =0 és bármely x, elég közel ahhoz x 1, az egyenlőtlenségek teljesülnek

f "(x)< 0 órakor x< x 1 , f "(x)> 0 órakor x> x 1 .

Majd a pont bal oldalán x 1 a függvény a jobb oldalon növekszik és csökken, tehát amikor x = x 1 függvény növekvőről csökkenőre megy, vagyis van maximuma.

Hasonlóképpen figyelembe vehetjük a pontokat x 2 és x 3 .

A fentiek mindegyike sematikusan ábrázolható a képen:

Szabály az y=f(x) függvény tanulmányozására szélsőségre

Keresse meg egy függvény tartományát f(x).

Keresse meg egy függvény első deriváltját f "(x).

Határozza meg ehhez a kritikus pontokat:

megtalálni az egyenlet valódi gyökereit f "(x)=0;

megtalálja az összes értéket x amelyre a származék f "(x) nem létezik.

Határozzuk meg a kritikus ponttól balra és jobbra eső derivált előjelét! Mivel a derivált előjele két kritikus pont között állandó marad, elegendő a derivált előjelét a kritikus ponttól egy pontban balra és egy ponttal jobbra meghatározni.

Számítsa ki a függvény értékét a szélsőpontokban!

Tekintsük egy folytonos függvény grafikonját y=f(x)ábrán látható.

Funkció értéke egy pontban x 1 nagyobb lesz, mint a függvényértékek az összes szomszédos pontban, mind balra, mind jobbra x 1 . Ebben az esetben azt mondjuk, hogy a függvénynek a pontja van x 1 maximum. Azon a ponton x A 3. függvénynek nyilván van maximuma is. Ha figyelembe vesszük a lényeget x 2, akkor a benne lévő függvény értéke kisebb, mint az összes szomszédos érték. Ebben az esetben azt mondjuk, hogy a függvénynek a pontja van x 2 minimum. Hasonlóan a lényeghez x 4 .

Funkció y=f(x) azon a ponton x 0 rendelkezik maximális, ha a függvény értéke ezen a ponton nagyobb, mint a pontot tartalmazó intervallum minden pontjában elért értékei x 0, azaz ha van egy pontnak ilyen környéke x 0, ami mindenkinek szól x≠x 0 , ehhez a szomszédsághoz tartozik az egyenlőtlenség f(x)<f(x 0 ) .

Funkció y=f(x) Megvan minimális azon a ponton x 0 , ha van egy pontnak ilyen környéke x 0 , ez mindenkinek szól x≠x 0 ehhez a szomszédsághoz tartozó egyenlőtlenség fennáll f(x)>f(x 0.

Azokat a pontokat, ahol a függvény eléri maximumát és minimumát, szélsőséges pontoknak nevezzük, a függvény értékeit pedig ezekben a pontokban a függvény szélsőértékeinek.

Figyeljünk arra, hogy egy szakaszon definiált függvény csak a vizsgált szakaszon belüli pontokban érheti el a maximumot és a minimumot.

Megjegyzendő, hogy ha egy függvénynek egy pontban van maximuma, ez nem jelenti azt, hogy azon a ponton a függvénynek van a legnagyobb értéke a teljes definíciós tartományban. A fent tárgyalt ábrán a pontban lévő függvény x 1-nek van maximuma, bár vannak olyan pontok, ahol a függvényértékek nagyobbak, mint a ponton x 1 . Különösen, f(x 1) < f(x 4) azaz. egy függvény minimuma nagyobb, mint a maximum. A maximum definíciójából csak az következik, hogy ez a függvény legnagyobb értéke a maximum ponthoz kellően közeli pontokban.

1. Tétel (A szélsőség létezésének szükséges feltétele.) Ha a differenciálható függvény y=f(x) pontban van x= x 0 extrémum, akkor a deriváltja ezen a ponton nulla lesz.

Bizonyíték. Hagyjuk, a határozottság kedvéért a pontnál x A 0 függvénynek maximuma van. Ekkor kellően kis lépésekben Δ x nekünk van f(x 0 + Δ x) 0 ) , azaz De aztán

Ezeket az egyenlőtlenségeket átengedjük a Δ-nél lévő határértékre x→ 0 és figyelembe véve, hogy a derivált f "(x 0) létezik, ezért a bal oldali határérték nem függ attól, hogyan Δ x→ 0, kapjuk: Δ-nél x → 0 – 0 f"(x 0) ≥ 0 a Δ-nél x → 0 + 0 f"(x 0) ≤ 0. Mivel f"(x 0) definiál egy számot, akkor ez a két egyenlőtlenség csak akkor kompatibilis, ha f"(x 0) = 0.

A bizonyított tétel kimondja, hogy a maximum és minimum pont csak az argumentum azon értékei között lehet, amelyeknél a derivált nullává válik.

Azt az esetet vizsgáltuk, amikor egy függvénynek egy adott szegmens minden pontján deriváltja van. Mi a helyzet azokban az esetekben, amikor a származékos termék nem létezik? Nézzünk példákat.

Példák.

y=|x|.
A függvénynek nincs deriváltja a ponton x=0 (ezen a ponton a függvény grafikonjának nincs definiált érintője), de ezen a ponton a függvénynek van minimuma, mivel y(0)=0, és mindenre x≠ 0y > 0.

A függvénynek nincs at deriváltja x=0, mivel pontnál a végtelenbe megy x=0. De ezen a ponton a függvénynek van maximuma.

A függvénynek nincs at deriváltja x=0, mivel nál nél x→0. Ezen a ponton a függvénynek nincs sem maximuma, sem minimuma. Igazán, f(x)=0 és at x<0f(x)<0, а при x>0f(x)>0.

A megadott példákból és a megfogalmazott tételből tehát világos, hogy egy függvénynek csak két esetben lehet szélsősége: 1) olyan pontokban, ahol a derivált létezik és egyenlő nullával; 2) azon a ponton, ahol a származék nem létezik.

Ha azonban valamikor x 0 ezt tudjuk f "(x 0 ) =0, akkor ebből nem lehet arra következtetni, hogy azon a ponton x 0 a függvénynek szélsőértéke van.

Például. .

De időszak x A =0 nem szélsőpont, mivel ettől a ponttól balra a függvényértékek a tengely alatt találhatók Ökör, és jobbra fent.

Egy függvény tartományából származó argumentum értékeit, ahol a függvény deriváltja eltűnik vagy nem létezik, nevezzük. kritikus pontok.

A fentiekből következik, hogy a függvény szélsőpontjai a kritikus pontok közé tartoznak, de nem minden kritikus pont szélsőpont. Ezért egy függvény szélsőértékének megtalálásához meg kell találni a függvény összes kritikus pontját, majd ezeket a pontokat külön-külön meg kell vizsgálni a maximum és a minimum szempontjából. Ezt a célt szolgálja a következő tétel.

2. Tétel (Elegendő feltétel a szélsőség létezéséhez.) Legyen a függvény folytonos a kritikus pontot tartalmazó intervallumon x 0, és ennek az intervallumnak minden pontján differenciálható (kivéve talán magát a pontot x 0). Ha ezen a ponton balról jobbra haladva a derivált előjelet vált pluszról mínuszra, akkor a pontban x = x A 0 függvénynek maximuma van. Ha áthaladáskor x 0 balról jobbra, a derivált mínuszról pluszra változtatja az előjelet, akkor a függvénynek ezen a ponton van minimuma.

Így ha

Bizonyíték. Először tegyük fel, hogy amikor áthaladunk x 0 a derivált az előjelet pluszról mínuszra változtatja, azaz. mindenki előtt x, közel a lényeghez x 0 f "(x)> 0 érte x< x 0 , f "(x)< 0 érte x> x 0 . Alkalmazzuk Lagrange tételét a különbségre f(x) - f(x 0 ) = f "(c)(x-x 0), hol c között fekszik xÉs x 0 .

Hadd x< x 0 . Akkor c< x 0 és f "c)> 0. Ezért f "(c)(x-x 0)< 0 és ezért
f(x) - f(x 0 )< 0, azaz f(x)< f(x 0 ).

Hadd x > x 0 . Akkor c>x 0 és f "(c)< 0. Eszközök f "(c)(x-x 0)< 0. Ezért f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Így minden értékre x elég közel ahhoz x 0 f(x)< f(x 0 ) . Ez pedig azt jelenti, hogy pont x A 0 függvénynek maximuma van.

A minimumtétel második részét hasonló módon bizonyítjuk.

Illusztráljuk ennek a tételnek a jelentését az ábrán. Hadd f "(x 1 ) =0 és bármely x, elég közel ahhoz x 1, az egyenlőtlenségek teljesülnek

f "(x)< 0 órakor x< x 1 , f "(x)> 0 órakor x> x 1 .

Majd a pont bal oldalán x 1 a függvény a jobb oldalon növekszik és csökken, tehát amikor x = x 1 függvény növekvőről csökkenőre megy, vagyis van maximuma.

Hasonlóképpen figyelembe vehetjük a pontokat x 2 és x 3 .

A fentiek mindegyike sematikusan ábrázolható a képen:

Szabály az y=f(x) függvény tanulmányozására szélsőségre

Keresse meg egy függvény tartományát f(x).

Keresse meg egy függvény első deriváltját f "(x).

Határozza meg ehhez a kritikus pontokat:
megtalálni az egyenlet valódi gyökereit f "(x)=0;

megtalálja az összes értéket x amelyre a származék f "(x) nem létezik.

Határozzuk meg a kritikus ponttól balra és jobbra eső derivált előjelét! Mivel a derivált előjele két kritikus pont között állandó marad, elegendő a derivált előjelét a kritikus ponttól egy pontban balra és egy ponttal jobbra meghatározni.

Számítsa ki a függvény értékét a szélsőpontokban!

Példák. Fedezze fel a minimum és maximum funkciókat.

EGY SZEGMENS FUNKCIÓJÁNAK MAXIMÁLIS ÉS LEGKISEBB ÉRTÉKEI

A legnagyobb egy függvény értéke egy intervallumon a legnagyobb az ezen az intervallumon lévő összes értéke közül, és a legkisebb– értékei közül a legkisebb.

Fontolja meg a funkciót y=f(x) folyamatos a szakaszon [ a, b]. Mint ismeretes, egy ilyen függvény akár a szakasz határán, akár azon belül éri el maximális és minimális értékét. Ha egy függvény legnagyobb vagy legkisebb értékét a szakasz egy belső pontjában érjük el, akkor ez az érték a függvény maximuma vagy minimuma, vagyis a kritikus pontokon érhető el.

Így a következőket kapjuk szabály egy függvény legnagyobb és legkisebb értékének megtalálására egy szegmensen[ a, b] :

Keresse meg a függvény összes kritikus pontját az intervallumban ( a, b), és számítsa ki a függvény értékeit ezeken a pontokon.

Számítsa ki a függvény értékeit a szegmens végén, amikor x = a, x = b.

Az összes kapott érték közül válassza ki a legnagyobbat és a legkisebbet.

Legyen a $z=f(x,y)$ függvény definiálva a $(x_0,y_0)$ pont valamelyik szomszédságában. Azt mondják, hogy $(x_0,y_0)$ egy (lokális) maximumpont, ha a $(x_0,y_0)$ pont valamelyik szomszédságában lévő $(x,y)$ minden pontra a $f(x,y) egyenlőtlenség elégedett< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, akkor a $(x_0,y_0)$ pontot (lokális) minimumpontnak nevezzük.

A maximális és minimum pontot gyakran nevezik általános kifejezésnek - szélsőséges pontoknak.

Ha $(x_0,y_0)$ egy maximális pont, akkor a $f(x_0,y_0)$ függvény értékét ezen a ponton a $z=f(x,y)$ függvény maximumának nevezzük. Ennek megfelelően a függvény minimumponti értékét a $z=f(x,y)$ függvény minimumának nevezzük. Egy függvény minimumát és maximumát egy közös kifejezés – a függvény szélsőértéke – egyesíti.

Algoritmus a $z=f(x,y)$ extrémum függvény tanulmányozására

Keresse meg a $\frac(\partial z)(\partial x)$ és $\frac(\partial z)(\partial y)$ parciális deriváltokat. Állítsa össze és oldja meg a $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 egyenletrendszert \ end(aligned) \right.$ Azokat a pontokat, amelyek koordinátái megfelelnek a megadott rendszernek, stacionáriusnak nevezzük.

Keresse meg a következőt: $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$, és számítsa ki a $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ minden állópontban. Ezt követően használja a következő sémát:
Ha $\Delta > 0$ és $\frac(\partial^2z)(\partial x^2) > 0$ (vagy $\frac(\partial^2z)(\partial y^2) > 0$), akkor a vizsgált pont a minimumpont.

Ha $\Delta > 0$ és $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.

Ha $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.

Ha $\Delta = 0$, akkor semmi határozott nem mondható a szélsőség jelenlétéről; további kutatásra van szükség.

Megjegyzés (kívánatos a szöveg teljesebb megértéséhez): show\hide

Ha $\Delta > 0$, akkor $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\) részleges^2z)(\partial x\partial y) \right)^2 > 0$. Ebből következik, hogy $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) ( \partial x\partial y)\right)^2 ≥ 0$. Azok. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Ha bizonyos mennyiségek szorzata nagyobb nullánál, akkor ezek a mennyiségek azonos előjelűek. Ez például ha $\frac(\partial^2z)(\partial x^2) > 0$, akkor $\frac(\partial^2z)(\partial y^2) > 0$. Röviden, ha $\Delta > 0$, akkor a $\frac(\partial^2z)(\partial x^2)$ és a $\frac(\partial^2z)(\partial y^2)$ előjele egybeesik .

1. számú példa

Vizsgálja meg a $z=4x^2-6xy-34x+5y^2+42y+7$ függvény szélsőértékét.

$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$
$$ \left \( \begin(igazított) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(igazított) \jobbra. $$
Csökkentsük ennek a rendszernek az egyes egyenleteit $2$-ral, és mozgassuk a számokat az egyenletek jobb oldalára:
$$ \bal \( \begin(igazított) & 4x-3y=17;\\ & -3x+5y=-21. \end(igazított) \jobbra. $$
Lineáris algebrai egyenletrendszert kaptunk. Ebben a helyzetben számomra a legkényelmesebbnek tűnik a Cramer módszer alkalmazása a kapott rendszer megoldására.
$$ \begin(aligned) & \Delta=\left| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\left| \begin(array) (cc) 17 & -3\\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\left| \begin(array) (cc) 4 & 17\\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(igazított) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$
A $x=2$, $y=-3$ értékek a $(2;-3)$ állópont koordinátái.
$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$
Számítsuk ki a $\Delta$ értékét:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$
Mivel a $\Delta > 0$ és a $\frac(\partial^2 z)(\partial x^2) > 0$, ezért a pont szerint $(2;-3)$ a $ függvény minimumpontja z$. A $z$ függvény minimumát úgy találjuk meg, hogy a $(2;-3)$ pont koordinátáit behelyettesítjük az adott függvénybe:
$$ z_(perc)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$
Válasz: $(2;-3)$ - minimum pont; $z_(perc)=-90 $.

2. példa

Vizsgálja meg a $z=x^3+3xy^2-15x-12y+1$ függvény szélsőértékét.

Követni fogjuk a fentieket. Először keressük meg az elsőrendű parciális származékokat:
$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y)=6xy-12. $$
Hozzuk létre a $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 egyenletrendszert. \end( igazítva) \jobbra.$:
$$ \left \( \begin(igazított) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(igazított) \jobbra. $$
Csökkentsük az első egyenletet 3-mal, a másodikat pedig 6-tal.
$$ \left \( \begin(aligned) & x^2+y^2-5=0;\\ & xy-2=0. \end(aligned) \right. $$
Ha $x=0$, akkor a második egyenlet ellentmondáshoz vezet: $0\cdot y-2=0$, $-2=0$. Innen a következtetés: $x\neq 0$. Ekkor a második egyenletből a következőt kapjuk: $xy=2$, $y=\frac(2)(x)$. Ha behelyettesítjük a $y=\frac(2)(x)$-t az első egyenletbe, akkor a következőt kapjuk:
$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$
Kaptunk egy bikvadratikus egyenletet. Elvégezzük a $t=x^2$ cserét (ami azt jelenti, hogy $t > 0$):
$$ t^2-5t+4=0;\\ \begin(igazított) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(igazított) $$
Ha $t=1$, akkor $x^2=1$. Ezért van két $x$ értékünk: $x_1=1$, $x_2=-1$. Ha $t=4$, akkor $x^2=4$, azaz. $x_3=2$, $x_4=-2$. Emlékezve, hogy $y=\frac(2)(x)$, a következőt kapjuk:
\begin(igazított) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2)=-1. \end(igazított)
Tehát négy állandó pontunk van: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Ezzel befejeződik az algoritmus első lépése.

Most kezdjük az algoritmussal. Keressük a másodrendű parciális deriváltokat:
$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$
Keressük meg a $\Delta$-t:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$
Most kiszámoljuk a $\Delta$ értékét minden korábban talált stacionárius pontban. Kezdjük a $M_1(1;2)$ pontból. Ezen a ponton a következőt kapjuk: $\Delta(M_1)=36(1^2-2^2)=-108$. $\Delta(M_1) óta< 0$, то согласно в точке $M_1$ экстремума нет.

Vizsgáljuk meg a $M_2(-1;-2)$ pontot. Ezen a ponton a következőt kapjuk: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. $\Delta(M_2) óta< 0$, то согласно в точке $M_2$ экстремума нет.

Vizsgáljuk meg a $M_3(2;1)$ pontot. Ezen a ponton kapjuk:
$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$
Mivel $\Delta(M_3) > 0$ és $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, akkor a $M_3(2; 1)$ a $z$ függvény minimális pontja. A $z$ függvény minimumát úgy találjuk meg, hogy a $M_3$ pont koordinátáit behelyettesítjük az adott függvénybe:
$$ z_(perc)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$
Marad a $M_4(-2;-1)$ pont feltárása. Ezen a ponton kapjuk:
$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$
Mivel $\Delta(M_4) > 0$ és $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$
Az extrémum vizsgálat befejeződött. Már csak a választ le kell írni.

Válasz:

$(2;1)$ - minimum pont, $z_(perc)=-27$;

$(-2;-1)$ - maximális pont, $z_(max)=29$.

jegyzet

Általános esetben nem szükséges a $\Delta$ értékét kiszámolni, mert minket csak az előjel érdekel, ennek a paraméternek nem a konkrét értéke. Például a fenti 2. számú példában a $M_3(2;1)$ pontban $\Delta=36\cdot(2^2-1^2)$ áll rendelkezésünkre. Itt nyilvánvaló, hogy $\Delta > 0$ (mivel mind a $36$, mind a $(2^2-1^2)$ faktor pozitív), és előfordulhat, hogy nem találunk $\Delta$ konkrét értéket. Igaz, a szabványos számításokhoz ez a megjegyzés haszontalan - ott megkövetelik, hogy a számításokat egy számra hozza :)

3. példa

Vizsgálja meg a $z=x^4+y^4-2x^2+4xy-2y^2+3$ függvény szélsőértékét.

Követni fogjuk. Először keressük meg az elsőrendű parciális származékokat:
$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$
Hozzuk létre a $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 egyenletrendszert. \end( igazítva) \jobbra.$:
$$ \left \( \begin (igazított) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(igazított) \jobbra. $$
Csökkentsük mindkét egyenletet 4 dollárral:
$$ \left \( \begin(igazított) & x^3-x+y=0;\\ & y^3+x-y=0. \end(igazított) \jobbra. $$
Adjuk hozzá az első egyenletet a másodikhoz, és fejezzük ki $y$-t $x$-ban:
$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$
Ha a rendszer első egyenletébe behelyettesítjük $y=-x$ értékét, akkor a következőt kapjuk:
$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$
A kapott egyenletből a következőt kapjuk: $x=0$ vagy $x^2-2=0$. A $x^2-2=0$ egyenletből az következik, hogy $x=-\sqrt(2)$ vagy $x=\sqrt(2)$. Tehát a $x$ három értéke található, nevezetesen: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Mivel $y=-x$, akkor $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.

A megoldás első lépése befejeződött. Három állópontot kaptunk: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .

Most kezdjük az algoritmussal. Keressük a másodrendű parciális deriváltokat:
$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$
Keressük meg a $\Delta$-t:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$
Most kiszámoljuk a $\Delta$ értékét minden korábban talált stacionárius pontban. Kezdjük a $M_1(0;0)$ pontból. Ezen a ponton a következőt kapjuk: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Mivel $\Delta(M_1) = 0$, ezért további kutatásra van szükség, mivel semmi határozottat nem lehet mondani a szélsőség jelenlétéről a vizsgált ponton. Hagyjuk most ezt a pontot, és térjünk át a többi pontra.

Vizsgáljuk meg a $M_2(-\sqrt(2),\sqrt(2))$ pontot. Ezen a ponton kapjuk:
\begin(igazított) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end(igazított)
Mivel $\Delta(M_2) > 0$ és $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, akkor a $M_2(-\) szerint sqrt(2),\sqrt(2))$ a $z$ függvény minimális pontja. A $z$ függvény minimumát úgy találjuk meg, hogy a $M_2$ pont koordinátáit behelyettesítjük az adott függvénybe:
$$ z_(perc)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$
Az előző ponthoz hasonlóan megvizsgáljuk a $M_3(\sqrt(2),-\sqrt(2))$ pontot. Ezen a ponton kapjuk:
\begin(igazított) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end(igazított)
Mivel $\Delta(M_3) > 0$ és $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, akkor a $M_3(\sqrt) szerint (2),-\sqrt(2))$ a $z$ függvény minimális pontja. A $z$ függvény minimumát úgy találjuk meg, hogy a $M_3$ pont koordinátáit behelyettesítjük az adott függvénybe:
$$ z_(perc)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2) ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$
Ideje visszatérni a $M_1(0;0)$ ponthoz, ahol $\Delta(M_1) = 0$. Eszerint további kutatásokra van szükség. Ez a kitérő kifejezés azt jelenti, hogy "csinálj, amit akarsz" :). Nincs általános mód az ilyen helyzetek megoldására, és ez érthető. Ha létezne ilyen módszer, már régen minden tankönyvben szerepelt volna. Addig is minden olyan ponthoz, ahol $\Delta = 0$, egy speciális megközelítést kell keresnünk. Nos, vizsgáljuk meg a függvény viselkedését a $M_1(0;0)$ pont közelében. Azonnal jegyezzük meg, hogy $z(M_1)=z(0;0)=3$. Tegyük fel, hogy $M_1(0;0)$ a minimumpont. Ekkor bármely $M$ pontra a $M_1(0;0)$ pont valamelyik szomszédságából megkapjuk a $z(M) > z(M_1)$, azaz. $z(M) > 3$. Mi van akkor, ha bármely környék olyan pontokat tartalmaz, amelyeknél $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Tekintsük azokat a pontokat, amelyekre $y=0$, azaz. $(x,0)$ alakú pontok. Ezeken a pontokon a $z$ függvény a következő értékeket veszi fel:
$$ z(x,0)=x^4+0^4-2x^2+4x\cpont 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x) ^2-2)+3. $$
Minden kellően kicsi $M_1(0;0)$ környéken van $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

De lehet, hogy a $M_1(0;0)$ pont a maximális pont? Ha ez így van, akkor a $M_1(0;0)$ bármely szomszédságából származó $M$ bármely pontra megkapjuk a $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3 dollár? Akkor biztosan nem lesz maximum a $M_1$ pontban.

Tekintsük azokat a pontokat, amelyekre $y=x$, azaz. $(x,x)$ alakú pontok. Ezeken a pontokon a $z$ függvény a következő értékeket veszi fel:
$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$
Mivel a $M_1(0;0)$ pont bármely szomszédságában van $2x^4 > 0$, akkor $2x^4+3 > 3$. Következtetés: a $M_1(0;0)$ pont bármely környéke olyan pontokat tartalmaz, amelyeknél $z > 3$, ezért a $M_1(0;0)$ pont nem lehet maximumpont.

A $M_1(0;0)$ pont nem maximum és nem is minimumpont. Következtetés: $M_1$ egyáltalán nem szélsőséges pont.

Válasz: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ a $z$ függvény minimális pontjai. Mindkét pontban $z_(min)=-5$.

Az x 0 pontot nevezzük maximális pont(minimális) f(x) függvényt, ha az x 0 pont valamelyik környezetében teljesül az f(x) ≤f(x 0) (f(x) ≥f(x 0)) egyenlőtlenség.
A függvény értékét ezen a ponton ennek megfelelően hívjuk meg maximális vagy minimális funkciókat. A maximum és minimum függvényeket egy közös név egyesíti extrémum funkciókat.
Egy függvény extrémumát ebben az értelemben gyakran nevezik helyi extrémum, hangsúlyozva azt a tényt, hogy ez a fogalom csak az x 0 pont kellően kis környezetéhez kapcsolódik. Ugyanazon az intervallumon egy függvénynek több lokális maximuma és minimuma lehet, amelyek nem feltétlenül esnek egybe globális maximum vagy minimális(azaz a függvény legnagyobb vagy legkisebb értéke a teljes intervallumban).
Az extrémumhoz szükséges feltétel. Ahhoz, hogy egy függvénynek egy pontban szélsőértéke legyen, szükséges, hogy a deriváltja ebben a pontban egyenlő legyen nullával, vagy ne létezzen.
A differenciálható függvények esetében ez a feltétel Fermat tételéből következik. Ezenkívül rendelkezik arról az esetről is, amikor egy függvény szélsőértéke van egy olyan ponton, ahol nem differenciálható.
Azokat a pontokat, ahol a szükséges szélsőfeltétel teljesül, hívjuk kritikai(vagy helyhez kötött differenciálható függvényhez). Ezeknek a pontoknak a függvény tartományán belül kell lenniük.
Így, ha bármely ponton van szélsőség, akkor ez a pont kritikus (szükséges feltétel). Vegye figyelembe, hogy ennek a fordítottja nem igaz. A kritikus pont nem feltétlenül extrémum, azaz. a megadott feltétel nem elegendő.
Az első elégséges feltétel az extrémumhoz. Ha egy bizonyos ponton áthaladva a differenciálható függvény deriváltja az előjelét pluszról mínuszra változtatja, akkor ez a függvény maximumpontja, ha pedig mínuszról pluszra, akkor ez a minimumpont.
Ennek a feltételnek a bizonyítása a monotonitás elégséges feltételéből következik (a derivált előjelének megváltozásakor vagy a függvény növekedéséből csökkenésbe, vagy csökkenésből növekedésbe való átmenet következik be).
A második elégséges feltétel az extrémumhoz. Ha egy kétszer differenciálható függvény első deriváltja egy ponton nulla, és a második derivált ezen a ponton pozitív, akkor ez a függvény minimumpontja; és ha a második derivált negatív, akkor ez a maximális pont.
Ennek a feltételnek a bizonyítása a monotonitás elégséges feltételén is alapul. Valójában, ha a második derivált pozitív, akkor az első derivált egy növekvő függvény. Mivel a kérdéses pontban egyenlő nullával, ezért az áthaladáskor az előjelet mínuszról pluszra változtatja, ami visszaadja a lokális minimum első elégséges feltételét. Hasonlóképpen, ha a második derivált negatív, akkor az első csökken, és az előjelet pluszról mínuszra változtatja, ami elégséges feltétele egy lokális maximumnak.
Függvény tanulmányozása szélsőséghez a megfogalmazott tételeknek megfelelően a következő szakaszokat tartalmazza:
1. Keresse meg az f`(x) függvény első deriváltját!
2. Ellenőrizze a szükséges extrémum feltétel teljesülését, pl. keressük meg az f(x) függvény azon kritikus pontjait, ahol az f`(x) = 0 vagy nem létezik.
3. Ellenőrizze az extrémum elégséges feltételének teljesülését, pl. vagy vizsgálja meg az egyes kritikus pontoktól balra és jobbra eső derivált előjelét, vagy keresse meg a második f``(x) deriváltot, és határozza meg annak előjelét minden kritikus pontban. Vonjon le következtetést a függvény szélsőségeinek jelenlétéről.
4. Keresse meg a függvény szélsőértékeit!
Egy függvény globális maximumának és minimumának megkeresése bizonyos időn belül nagy gyakorlati jelentősége is van. A probléma megoldása egy szakaszon a Weierstrass-tételen alapul, amely szerint a folytonos függvény a legnagyobb és a legkisebb értékeit egy szakaszon veszi fel. Mind az extrém pontokon, mind a szegmens végén elérhetők. Ezért a megoldás a következő lépéseket tartalmazza:
1. Keresse meg az f`(x) függvény deriváltját!
2. Keresse meg az f(x) függvény kritikus pontjait, ahol az f`(x) = 0 vagy nem létezik.
3. Keresse meg a függvény értékeit a kritikus pontokon és a szegmens végén, és válassza ki közülük a legnagyobbat és a legkisebbet.

Ez a matematika egy meglehetősen érdekes része, amellyel abszolút minden végzős és diák találkozik. A matant azonban nem mindenki szereti. Vannak, akik még az alapvető dolgokat sem tudják megérteni, mint például egy szokásosnak tűnő függvénytanulmány. Ez a cikk egy ilyen mulasztást hivatott korrigálni. Szeretne többet megtudni a függvényelemzésről? Szeretné tudni, mik azok a szélsőséges pontok, és hogyan lehet megtalálni őket? Akkor ez a cikk neked szól.
Egy függvény grafikonjának tanulmányozása
Először is érdemes megérteni, miért szükséges egyáltalán elemezni a grafikont. Vannak egyszerű függvények, amelyeket nem nehéz megrajzolni. Egy ilyen függvény szembetűnő példája a parabola. Nem lesz nehéz grafikont rajzolni. Mindössze egy egyszerű transzformációval meg kell találni azokat a számokat, amelyeknél a függvény 0 értéket vesz fel. És elvileg ennyit kell tudnia egy parabola grafikonjának megrajzolásához.
De mi van akkor, ha a grafikon ábrázolásához szükséges függvény sokkal összetettebb? Mivel az összetett függvények tulajdonságai nem egészen nyilvánvalóak, szükséges egy teljes elemzés elvégzése. Csak ezután lehet a függvényt grafikusan ábrázolni. Hogy kell ezt csinálni? Ebben a cikkben megtalálhatja a választ erre a kérdésre.
Funkcióelemzési terv
Az első dolog, amit tennünk kell, hogy egy felületes vizsgálatot végzünk a függvényről, amely során megtaláljuk a definíciós tartományt. Tehát kezdjük sorban. A definíciós tartomány az értékkészlet, amellyel a függvény definiálva van. Egyszerűen fogalmazva, ezek azok a számok, amelyek az x helyett egy függvényben használhatók. A hatókör meghatározásához csak meg kell néznie a rekordot. Például nyilvánvaló, hogy az y (x) = x 3 + x 2 - x + 43 függvénynek van egy definíciós tartománya, amely a valós számok halmaza. Nos, az (x 2 - 2x)/x függvényekkel minden egy kicsit más. Mivel a nevezőben lévő szám nem lehet egyenlő 0-val, ennek a függvénynek a definíciós tartománya a nullától eltérő minden valós szám lesz.
Ezután meg kell találnia a függvény úgynevezett nulláit. Ezek azok az argumentumértékek, amelyeknél a teljes függvény nulla értéket vesz fel. Ehhez a függvényt nullával kell egyenlővé tenni, részletesen át kell gondolni, és végre kell hajtani néhány átalakítást. Vegyük a már ismert y(x) = (x 2 - 2x)/x függvényt. Az iskolai kurzusból tudjuk, hogy egy tört egyenlő 0-val, ha a számláló nullával egyenlő. Ezért eldobjuk a nevezőt, és a számlálóval kezdünk dolgozni, egyenlővé téve azt nullával. Azt kapjuk, hogy x 2 - 2x = 0, és x-et zárójelbe teszünk. Ebből következik, hogy x (x - 2) = 0. Ennek eredményeként azt találjuk, hogy a függvényünk egyenlő nullával, ha x értéke 0 vagy 2.
Egy függvény grafikonjának vizsgálatakor sokan extrémpontok formájában találkoznak problémákkal. És ez furcsa. Végül is a szélsőségek meglehetősen egyszerű téma. Ne higgy nekem? Győződjön meg róla, ha elolvassa a cikk ezen részét, amelyben a minimális és maximális pontokról fogunk beszélni.
Először is érdemes megérteni, mi az extrémum. Az extrémum az a határérték, amelyet egy függvény elér a grafikonon. Kiderült, hogy két szélső érték van - a maximum és a minimum. Az érthetőség kedvéért nézze meg a fenti képet. A vizsgált területen a -1 pont az y (x) = x 5 - 5x függvény maximuma, ennek megfelelően az 1. pont a minimuma.
Ezenkívül ne keverje össze a fogalmakat. A függvény szélsőpontjai azok az argumentumok, amelyeknél egy adott függvény szélsőértéket kap. Az extrémum viszont egy függvény minimumának és maximumának az értéke. Vegyük például újra a fenti ábrát. -1 és 1 a függvény szélsőpontja, a 4 és -4 pedig maguk a szélsőpontok.
A szélsőséges pontok megtalálása
De hogyan lehet megtalálni egy függvény szélsőpontját? Minden nagyon egyszerű. Az első dolog, hogy meg kell keresni az egyenlet deriváltját. Tegyük fel, hogy megkaptuk a feladatot: „Keressük meg az y (x) függvény szélsőpontjait, x az argumentum az érthetőség kedvéért vegyük az y (x) = x 3 + 2x 2 + x + 54 függvényt. kapjuk a következő egyenletet: 3x 2 + 4x + 1. Ennek eredményeként van egy standard másodfokú egyenletünk, csak annyit kell tenni, hogy egyenlővé kell tenni a nullával, és meg kell találni a gyököket, mivel a diszkrimináns nagyobb, mint nulla (D = 16 - 12 = 4), ezt az egyenletet két gyök határozza meg, és két értéket kapunk: 1/3 és -1 ki melyik pont a maximum és melyik a minimum. 1. Helyettesítsük be ezt az értéket az y(-2) = 12 - 8 + 1 = 5 egyenletbe. Ez azt jelenti, hogy az 1/3-tól -1-ig terjedő intervallumban a függvény növekszik. Ez viszont azt jelenti, hogy a mínusz végtelentől az 1/3-ig és a -1-től a plusz végtelenig terjedő intervallumokon a függvény csökken. Ebből arra következtethetünk, hogy az 1/3 szám a függvény minimumpontja a vizsgált intervallumon, és -1 a maximum pont.
Azt is érdemes megjegyezni, hogy az Egységes Államvizsgához nem csak az extrém pontok megtalálása szükséges, hanem valamilyen művelet elvégzése is velük (összeadás, szorzás stb.). Éppen ezért érdemes kiemelt figyelmet fordítani a probléma körülményeire. Hiszen a figyelmetlenség miatt pontokat veszíthet.