Βρείτε και εξερευνήστε τα ακραία σημεία της συνάρτησης. Το δεύτερο σημάδι ενός άκρου μιας συνάρτησης
Εισαγωγή
Σε πολλούς τομείς της επιστήμης και σε πρακτικές δραστηριότητες, κάποιος συχνά πρέπει να αντιμετωπίσει το πρόβλημα της εύρεσης του άκρου μιας συνάρτησης. Γεγονός είναι ότι πολλά τεχνικά, οικονομικά κ.λπ. Οι διαδικασίες μοντελοποιούνται από μια συνάρτηση ή πολλές συναρτήσεις που εξαρτώνται από μεταβλητές - παράγοντες που επηρεάζουν την κατάσταση του φαινομένου που μοντελοποιείται. Απαιτείται να βρεθούν τα άκρα τέτοιων συναρτήσεων προκειμένου να προσδιοριστεί η βέλτιστη (ορθολογική) κατάσταση και έλεγχος διαδικασίας. Έτσι, στα οικονομικά, τα προβλήματα ελαχιστοποίησης του κόστους ή μεγιστοποίησης των κερδών συχνά λύνονται - το μικροοικονομικό πρόβλημα της εταιρείας. Σε αυτή την εργασία, δεν εξετάζουμε ζητήματα μοντελοποίησης, αλλά εξετάζουμε μόνο αλγόριθμους για την αναζήτηση ακραίων συναρτήσεων στην απλούστερη έκδοση, όταν δεν επιβάλλονται περιορισμοί στις μεταβλητές (βελτιστοποίηση χωρίς όρους) και το άκρο αναζητείται μόνο για μία αντικειμενική συνάρτηση.
ΑΚΡΩΣ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
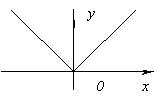
Θεωρήστε τη γραφική παράσταση μιας συνεχούς συνάρτησης y=f(x)φαίνεται στο σχήμα. Τιμή συνάρτησης σε ένα σημείο ΧΤο 1 θα είναι μεγαλύτερο από τις τιμές συνάρτησης σε όλα τα γειτονικά σημεία τόσο στα αριστερά όσο και στα δεξιά του Χ 1 . Σε αυτή την περίπτωση λέμε ότι η συνάρτηση έχει στο σημείο Χ 1 μέγιστο. Στο σημείο ΧΗ συνάρτηση 3 προφανώς έχει επίσης ένα μέγιστο. Αν αναλογιστούμε το σημείο Χ 2, τότε η τιμή της συνάρτησης σε αυτό είναι μικρότερη από όλες τις γειτονικές τιμές. Σε αυτή την περίπτωση λέμε ότι η συνάρτηση έχει στο σημείο Χ 2 τουλάχιστον. Το ίδιο και για την ουσία Χ 4 .
Λειτουργία y=f(x)στο σημείο Χ 0 έχει ανώτατο όριο, εάν η τιμή της συνάρτησης σε αυτό το σημείο είναι μεγαλύτερη από τις τιμές της σε όλα τα σημεία κάποιου διαστήματος που περιέχουν το σημείο Χ 0, δηλ. αν υπάρχει τέτοια γειτονιά ενός σημείου Χ 0, που είναι για όλους Χ≠Χ 0 , που ανήκει σε αυτή τη γειτονιά, η ανισότητα ισχύει f(x)<f(x 0 ) .
Λειτουργία y=f(x)Εχει ελάχιστοστο σημείο Χ 0 , αν υπάρχει τέτοια γειτονιά ενός σημείου Χ 0 , αυτό είναι για όλους Χ≠Χ 0 που ανήκει σε αυτή τη γειτονιά, ισχύει η ανισότητα f(x)>f(x 0.
Τα σημεία στα οποία η συνάρτηση φτάνει στο μέγιστο και το ελάχιστο ονομάζονται ακραία σημεία και οι τιμές της συνάρτησης σε αυτά τα σημεία ονομάζονται άκρα της συνάρτησης.
Ας δώσουμε προσοχή στο γεγονός ότι μια συνάρτηση που ορίζεται σε ένα τμήμα μπορεί να φτάσει στο μέγιστο και το ελάχιστο μόνο σε σημεία που περιέχονται στο υπό εξέταση τμήμα.
Σημειώστε ότι εάν μια συνάρτηση έχει μέγιστο σε ένα σημείο, αυτό δεν σημαίνει ότι σε εκείνο το σημείο η συνάρτηση έχει τη μεγαλύτερη τιμή σε ολόκληρο τον τομέα ορισμού. Στο σχήμα που συζητήθηκε παραπάνω, η συνάρτηση στο σημείο ΧΤο 1 έχει μέγιστο, αν και υπάρχουν σημεία στα οποία οι τιμές της συνάρτησης είναι μεγαλύτερες από το σημείο Χ 1 . Συγκεκριμένα, φά(Χ 1) < φά(Χ 4) δηλ. το ελάχιστο μιας συνάρτησης είναι μεγαλύτερο από το μέγιστο. Από τον ορισμό του μέγιστου προκύπτει μόνο ότι αυτή είναι η μεγαλύτερη τιμή της συνάρτησης σε σημεία αρκετά κοντά στο μέγιστο σημείο.
Θεώρημα 1. (Απαραίτητη προϋπόθεση για την ύπαρξη ακρότατου.) Αν η διαφοροποιήσιμη συνάρτηση y=f(x)έχει στο σημείο x= x 0 άκρο, τότε η παράγωγός του σε αυτό το σημείο γίνεται μηδέν.
Απόδειξη. Ας, για βεβαιότητα, στο σημείο ΧΗ συνάρτηση 0 έχει μέγιστο. Στη συνέχεια, για αρκετά μικρές αυξήσεις Δ Χέχουμε f(x 0 + Δ Χ)
Περνώντας σε αυτές τις ανισότητες στο όριο στο Δ Χ→ 0 και λαμβάνοντας υπόψη ότι η παράγωγος φά "(Χ 0) υπάρχει, και επομένως το όριο στα αριστερά δεν εξαρτάται από το πώς Δ Χ→ 0, παίρνουμε: στο Δ Χ → 0 – 0 φά"(Χ 0) ≥ 0 a στο Δ Χ → 0 + 0 φά"(Χ 0) ≤ 0. Αφού φά"(Χ 0) ορίζει έναν αριθμό, τότε αυτές οι δύο ανισότητες είναι συμβατές μόνο αν φά"(Χ 0) = 0.
Το αποδεδειγμένο θεώρημα δηλώνει ότι τα μέγιστα και τα ελάχιστα σημεία μπορούν να είναι μόνο μεταξύ εκείνων των τιμών του ορίσματος στις οποίες η παράγωγος γίνεται μηδέν.
Θεωρήσαμε την περίπτωση που μια συνάρτηση έχει παράγωγο σε όλα τα σημεία ενός συγκεκριμένου τμήματος. Ποια είναι η κατάσταση σε περιπτώσεις που το παράγωγο δεν υπάρχει; Ας δούμε παραδείγματα.
y=|Χ|.
Η συνάρτηση δεν έχει παράγωγο στο σημείο Χ=0 (σε αυτό το σημείο η γραφική παράσταση της συνάρτησης δεν έχει καθορισμένη εφαπτομένη), αλλά σε αυτό το σημείο η συνάρτηση έχει ελάχιστο, αφού y(0)=0 και για όλα Χ≠ 0y > 0.
δεν έχει παράγωγο στο Χ=0, αφού πηγαίνει στο άπειρο στο Χ=0. Αλλά σε αυτό το σημείο η συνάρτηση έχει ένα μέγιστο. δεν έχει παράγωγο στο Χ=0, αφού στις Χ→0. Σε αυτό το σημείο η συνάρτηση δεν έχει ούτε μέγιστο ούτε ελάχιστο. Πραγματικά, f(x)=0 και σε Χ<0f(x)<0, а при Χ>0f(x)>0.Έτσι, από τα παραδείγματα που δίνονται και το θεώρημα που διατυπώθηκε, είναι σαφές ότι μια συνάρτηση μπορεί να έχει άκρο μόνο σε δύο περιπτώσεις: 1) σε σημεία όπου υπάρχει η παράγωγος και είναι ίση με μηδέν. 2) στο σημείο που δεν υπάρχει το παράγωγο.
Ωστόσο, αν κάποια στιγμή Χ 0 το ξέρουμε αυτό f" (χ 0 ) =0, τότε δεν μπορεί κανείς να συμπεράνει από αυτό ότι στο σημείο Χ 0 η συνάρτηση έχει ακρότατο.
Για παράδειγμα.
.Αλλά περίοδος ΧΤο =0 δεν είναι ένα ακραίο σημείο, καθώς στα αριστερά αυτού του σημείου οι τιμές συναρτήσεων βρίσκονται κάτω από τον άξονα Βόδι, και πάνω δεξιά.
Οι τιμές του ορίσματος από τον τομέα της συνάρτησης στην οποία η παράγωγος της συνάρτησης εξαφανίζεται ή δεν υπάρχει ονομάζονται κρίσιμα σημεία.
Από όλα τα παραπάνω προκύπτει ότι τα ακραία σημεία της συνάρτησης είναι μεταξύ των κρίσιμων σημείων και, ωστόσο, δεν είναι κάθε κρίσιμο σημείο ακρότατο. Επομένως, για να βρείτε το άκρο μιας συνάρτησης, πρέπει να βρείτε όλα τα κρίσιμα σημεία της συνάρτησης και στη συνέχεια να εξετάσετε κάθε ένα από αυτά τα σημεία ξεχωριστά για μέγιστο και ελάχιστο. Το παρακάτω θεώρημα εξυπηρετεί αυτόν τον σκοπό.
Θεώρημα 2. (Μια επαρκής συνθήκη για την ύπαρξη ακρότατου.) Έστω η συνάρτηση συνεχής σε κάποιο διάστημα που περιέχει το κρίσιμο σημείο Χ 0, και είναι διαφοροποιήσιμο σε όλα τα σημεία αυτού του διαστήματος (εκτός, ίσως, από το ίδιο το σημείο Χ 0). Εάν, όταν μετακινείται από αριστερά προς τα δεξιά σε αυτό το σημείο, η παράγωγος αλλάζει πρόσημο από συν σε πλην, τότε στο σημείο Χ = ΧΗ συνάρτηση 0 έχει μέγιστο. Εάν, κατά τη διέλευση από Χ 0 από αριστερά προς τα δεξιά, η παράγωγος αλλάζει πρόσημο από μείον σε συν, τότε η συνάρτηση έχει ένα ελάχιστο σε αυτό το σημείο.
Έτσι, εάν
f "(x)>0 στο Χ<Χ 0 και f "(x)< 0 σε x> x 0, λοιπόν Χ 0 – μέγιστος βαθμός.
στο Χ<Χ 0 και f "(x)> 0 σε x> x 0, λοιπόν Χ 0 – ελάχιστος βαθμός.Απόδειξη. Ας υποθέσουμε πρώτα ότι κατά τη διέλευση Χ 0 η παράγωγος αλλάζει πρόσημο από συν σε πλην, δηλ. μπροστά σε όλους Χ, κοντά στο σημείο Χ 0 f "(x)> 0 για Χ< x 0 , f "(x)< 0 για x> x 0 . Ας εφαρμόσουμε το θεώρημα του Lagrange στη διαφορά f(x) - f(x 0 ) = f "(c) (x- x 0), όπου ντοβρίσκεται ανάμεσα ΧΚαι Χ 0 .
Αφήνω Χ< x 0 . Επειτα ντο< x 0 και f "(c)> 0. Να γιατί f "(c) (x- x 0)< 0 και επομένως
f(x) - f(x 0 )< 0, δηλ. f(x)< f(x 0 ).
Αφήνω x > x 0 . Επειτα c>x 0 και f "(c)< 0. Που σημαίνει f "(c) (x- x 0)< 0. Να γιατί f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
Έτσι, για όλες τις αξίες Χαρκετά κοντά σε Χ 0 f(x)< f(x 0 ) . Και αυτό σημαίνει ότι στο σημείο ΧΗ συνάρτηση 0 έχει μέγιστο.
Το δεύτερο μέρος του ελάχιστου θεωρήματος αποδεικνύεται με παρόμοιο τρόπο.
Ας δείξουμε την έννοια αυτού του θεωρήματος στο σχήμα. Αφήνω f" (χ 1 ) =0 και για οποιαδήποτε Χ,αρκετά κοντά σε Χ 1, οι ανισότητες ικανοποιούνται
f "(x)< 0 σε Χ< x 1 , f "(x)> 0 σε x> x 1 .
Στη συνέχεια στα αριστερά του σημείου Χ 1 η συνάρτηση αυξάνεται και μειώνεται στα δεξιά, επομένως, όταν Χ = Χ 1 συνάρτηση πηγαίνει από αύξουσα σε φθίνουσα, δηλαδή έχει μέγιστο.
Ομοίως, μπορούμε να εξετάσουμε σημεία Χ 2 και Χ 3 .
Όλα τα παραπάνω μπορούν να απεικονιστούν σχηματικά στην εικόνα:
Κανόνας για τη μελέτη της συνάρτησης y=f(x) για ακρότατο
Βρείτε τον τομέα μιας συνάρτησης f(x).
Βρείτε την πρώτη παράγωγο μιας συνάρτησης f "(x).
Προσδιορίστε κρίσιμα σημεία για αυτό:
βρείτε τις πραγματικές ρίζες της εξίσωσης f "(x)=0;
βρείτε όλες τις τιμές Χγια την οποία το παράγωγο f "(x)δεν υπάρχει.
Προσδιορίστε το πρόσημο της παραγώγου αριστερά και δεξιά του κρίσιμου σημείου. Εφόσον το πρόσημο της παραγώγου παραμένει σταθερό μεταξύ δύο κρίσιμων σημείων, αρκεί να προσδιορίσουμε το πρόσημο της παραγώγου σε ένα σημείο προς τα αριστερά και ένα σημείο προς τα δεξιά του κρίσιμου σημείου.
Υπολογίστε την τιμή της συνάρτησης στα ακραία σημεία.
Θεωρήστε τη γραφική παράσταση μιας συνεχούς συνάρτησης y=f(x)φαίνεται στο σχήμα.
Τιμή συνάρτησης σε ένα σημείο ΧΤο 1 θα είναι μεγαλύτερο από τις τιμές συνάρτησης σε όλα τα γειτονικά σημεία τόσο στα αριστερά όσο και στα δεξιά του Χ 1 . Σε αυτή την περίπτωση λέμε ότι η συνάρτηση έχει στο σημείο Χ 1 μέγιστο. Στο σημείο ΧΗ συνάρτηση 3 προφανώς έχει επίσης ένα μέγιστο. Αν αναλογιστούμε το σημείο Χ 2, τότε η τιμή της συνάρτησης σε αυτό είναι μικρότερη από όλες τις γειτονικές τιμές. Σε αυτή την περίπτωση λέμε ότι η συνάρτηση έχει στο σημείο Χ 2 τουλάχιστον. Το ίδιο και για την ουσία Χ 4 .
Λειτουργία y=f(x)στο σημείο Χ 0 έχει ανώτατο όριο, εάν η τιμή της συνάρτησης σε αυτό το σημείο είναι μεγαλύτερη από τις τιμές της σε όλα τα σημεία κάποιου διαστήματος που περιέχουν το σημείο Χ 0, δηλ. αν υπάρχει τέτοια γειτονιά ενός σημείου Χ 0, που είναι για όλους Χ≠Χ 0 , που ανήκει σε αυτή τη γειτονιά, η ανισότητα ισχύει f(x)<f(x 0 ) .
Λειτουργία y=f(x)Εχει ελάχιστοστο σημείο Χ 0 , αν υπάρχει τέτοια γειτονιά ενός σημείου Χ 0 , αυτό είναι για όλους Χ≠Χ 0 που ανήκει σε αυτή τη γειτονιά, ισχύει η ανισότητα f(x)>f(x 0.
Τα σημεία στα οποία η συνάρτηση φτάνει στο μέγιστο και το ελάχιστο της ονομάζονται ακραία σημεία και οι τιμές της συνάρτησης σε αυτά τα σημεία ονομάζονται άκρα της συνάρτησης.
Ας δώσουμε προσοχή στο γεγονός ότι μια συνάρτηση που ορίζεται σε ένα τμήμα μπορεί να φτάσει στο μέγιστο και στο ελάχιστο μόνο σε σημεία που περιέχονται στο υπό εξέταση τμήμα.
Σημειώστε ότι εάν μια συνάρτηση έχει μέγιστο σε ένα σημείο, αυτό δεν σημαίνει ότι σε εκείνο το σημείο η συνάρτηση έχει τη μεγαλύτερη τιμή σε ολόκληρο τον τομέα ορισμού. Στο σχήμα που συζητήθηκε παραπάνω, η συνάρτηση στο σημείο ΧΤο 1 έχει μέγιστο, αν και υπάρχουν σημεία στα οποία οι τιμές της συνάρτησης είναι μεγαλύτερες από το σημείο Χ 1 . Συγκεκριμένα, φά(Χ 1) < φά(Χ 4) δηλ. το ελάχιστο μιας συνάρτησης είναι μεγαλύτερο από το μέγιστο. Από τον ορισμό του μέγιστου προκύπτει μόνο ότι αυτή είναι η μεγαλύτερη τιμή της συνάρτησης σε σημεία αρκετά κοντά στο μέγιστο σημείο.
Θεώρημα 1. (Απαραίτητη προϋπόθεση για την ύπαρξη ακρότατου.)Αν η διαφοροποιήσιμη συνάρτηση y=f(x)έχει στο σημείο x= x 0 άκρο, τότε η παράγωγός του σε αυτό το σημείο γίνεται μηδέν.
Απόδειξη. Ας, για βεβαιότητα, στο σημείο ΧΗ συνάρτηση 0 έχει μέγιστο. Στη συνέχεια, για αρκετά μικρές αυξήσεις Δ Χέχουμε f(x 0 + Δ Χ)
Περνώντας σε αυτές τις ανισότητες στο όριο στο Δ Χ→ 0 και λαμβάνοντας υπόψη ότι η παράγωγος φά "(Χ 0) υπάρχει, και επομένως το όριο στα αριστερά δεν εξαρτάται από το πώς Δ Χ→ 0, παίρνουμε: στο Δ Χ → 0 – 0 φά"(Χ 0) ≥ 0 a στο Δ Χ → 0 + 0 φά"(Χ 0) ≤ 0. Αφού φά"(Χ 0) ορίζει έναν αριθμό, τότε αυτές οι δύο ανισότητες είναι συμβατές μόνο αν φά"(Χ 0) = 0.
Το αποδεδειγμένο θεώρημα δηλώνει ότι τα μέγιστα και ελάχιστα σημεία μπορούν να είναι μόνο μεταξύ εκείνων των τιμών του επιχειρήματος στις οποίες η παράγωγος γίνεται μηδέν.
Θεωρήσαμε την περίπτωση που μια συνάρτηση έχει παράγωγο σε όλα τα σημεία ενός συγκεκριμένου τμήματος. Ποια είναι η κατάσταση σε περιπτώσεις που το παράγωγο δεν υπάρχει; Ας δούμε παραδείγματα.
Παραδείγματα.
- y=|Χ|.
Η συνάρτηση δεν έχει παράγωγο στο σημείο Χ=0 (σε αυτό το σημείο η γραφική παράσταση της συνάρτησης δεν έχει καθορισμένη εφαπτομένη), αλλά σε αυτό το σημείο η συνάρτηση έχει ελάχιστο, αφού y(0)=0 και για όλα Χ≠ 0y > 0.
- Αφήνω Χ< x
0 . Επειτα ντο< x
0 και f "(c)> 0.
Να γιατί f "(c) (x- x 0)<
0 και επομένως
f(x) - f(x 0 )< 0, δηλ. f(x)< f(x 0 ).
- Αφήνω x > x 0 . Επειτα c>x 0 και f "(c)< 0. Που σημαίνει f "(c) (x- x 0)< 0. Να γιατί f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Βρείτε τον τομέα μιας συνάρτησης f(x).
- Βρείτε την πρώτη παράγωγο μιας συνάρτησης f "(x).
- Προσδιορίστε κρίσιμα σημεία για αυτό:
- βρείτε τις πραγματικές ρίζες της εξίσωσης f "(x)=0;
- βρείτε όλες τις τιμές Χγια την οποία το παράγωγο f "(x)δεν υπάρχει.
- Προσδιορίστε το πρόσημο της παραγώγου αριστερά και δεξιά του κρίσιμου σημείου. Εφόσον το πρόσημο της παραγώγου παραμένει σταθερό μεταξύ δύο κρίσιμων σημείων, αρκεί να προσδιορίσουμε το πρόσημο της παραγώγου σε ένα σημείο προς τα αριστερά και ένα σημείο προς τα δεξιά του κρίσιμου σημείου.
- Υπολογίστε την τιμή της συνάρτησης στα ακραία σημεία.
- Βρείτε όλα τα κρίσιμα σημεία της συνάρτησης στο διάστημα ( α, β) και υπολογίστε τις τιμές συνάρτησης σε αυτά τα σημεία.
- Υπολογίστε τις τιμές της συνάρτησης στα άκρα του τμήματος όταν x = a, x = b.
- Από όλες τις λαμβανόμενες τιμές, επιλέξτε τη μεγαλύτερη και τη μικρότερη.
Η συνάρτηση δεν έχει παράγωγο στο Χ=0, αφού πηγαίνει στο άπειρο στο Χ=0. Αλλά σε αυτό το σημείο η συνάρτηση έχει μέγιστο.

Η συνάρτηση δεν έχει παράγωγο στο Χ=0, αφού ![]() στο Χ→0. Σε αυτό το σημείο η συνάρτηση δεν έχει ούτε μέγιστο ούτε ελάχιστο. Πραγματικά, f(x)=0 και σε Χ<0f(x)<0, а при Χ>0f(x)>0.
στο Χ→0. Σε αυτό το σημείο η συνάρτηση δεν έχει ούτε μέγιστο ούτε ελάχιστο. Πραγματικά, f(x)=0 και σε Χ<0f(x)<0, а при Χ>0f(x)>0.

Έτσι, από τα παραδείγματα που δίνονται και το θεώρημα που διατυπώθηκε, είναι σαφές ότι μια συνάρτηση μπορεί να έχει άκρο μόνο σε δύο περιπτώσεις: 1) σε σημεία όπου υπάρχει η παράγωγος και είναι ίση με μηδέν. 2) στο σημείο που δεν υπάρχει το παράγωγο.
Ωστόσο, αν κάποια στιγμή Χ 0 το ξέρουμε αυτό f" (χ 0 ) =0, τότε δεν μπορεί κανείς να συμπεράνει από αυτό ότι στο σημείο Χ 0 η συνάρτηση έχει ακρότατο.
Για παράδειγμα. ![]() .
.

Αλλά περίοδος ΧΤο =0 δεν είναι ένα ακραίο σημείο, καθώς στα αριστερά αυτού του σημείου οι τιμές συνάρτησης βρίσκονται κάτω από τον άξονα Βόδι, και πάνω δεξιά.
Οι τιμές του ορίσματος από τον τομέα της συνάρτησης στην οποία η παράγωγος της συνάρτησης εξαφανίζεται ή δεν υπάρχει ονομάζονται κρίσιμα σημεία.
Από όλα τα παραπάνω προκύπτει ότι τα ακραία σημεία της συνάρτησης είναι μεταξύ των κρίσιμων σημείων και, ωστόσο, δεν είναι κάθε κρίσιμο σημείο ακρότατο. Επομένως, για να βρείτε το άκρο μιας συνάρτησης, πρέπει να βρείτε όλα τα κρίσιμα σημεία της συνάρτησης και στη συνέχεια να εξετάσετε κάθε ένα από αυτά τα σημεία ξεχωριστά για μέγιστο και ελάχιστο. Το παρακάτω θεώρημα εξυπηρετεί αυτόν τον σκοπό.
Θεώρημα 2. (Επαρκής συνθήκη για την ύπαρξη ακρότατου.)Αφήστε τη συνάρτηση να είναι συνεχής σε κάποιο διάστημα που περιέχει το κρίσιμο σημείο Χ 0, και είναι διαφοροποιήσιμο σε όλα τα σημεία αυτού του διαστήματος (εκτός, ίσως, από το ίδιο το σημείο Χ 0). Εάν, όταν μετακινείται από αριστερά προς τα δεξιά σε αυτό το σημείο, η παράγωγος αλλάζει πρόσημο από συν σε πλην, τότε στο σημείο Χ = ΧΗ συνάρτηση 0 έχει μέγιστο. Εάν, κατά τη διέλευση από Χ 0 από αριστερά προς τα δεξιά, η παράγωγος αλλάζει πρόσημο από μείον σε συν, τότε η συνάρτηση έχει ένα ελάχιστο σε αυτό το σημείο.
Έτσι, εάν
Απόδειξη. Ας υποθέσουμε πρώτα ότι κατά τη διέλευση Χ 0 η παράγωγος αλλάζει πρόσημο από συν σε πλην, δηλ. μπροστά σε όλους Χ, κοντά στο σημείο Χ 0 f "(x)> 0 για Χ< x 0 , f "(x)< 0 για x> x 0 . Ας εφαρμόσουμε το θεώρημα του Lagrange στη διαφορά f(x) - f(x 0 ) = f "(c) (x- x 0), όπου ντοβρίσκεται ανάμεσα ΧΚαι Χ 0 .
Έτσι, για όλες τις αξίες Χαρκετά κοντά σε Χ 0 f(x)< f(x 0 ) . Και αυτό σημαίνει ότι στο σημείο ΧΗ συνάρτηση 0 έχει μέγιστο.
Το δεύτερο μέρος του ελάχιστου θεωρήματος αποδεικνύεται με παρόμοιο τρόπο.

Ας δείξουμε την έννοια αυτού του θεωρήματος στο σχήμα. Αφήνω f" (χ 1 ) =0 και για οποιαδήποτε Χ,αρκετά κοντά σε Χ 1, οι ανισότητες ικανοποιούνται
f "(x)< 0 σε Χ< x 1 , f "(x)> 0 σε x> x 1 .
Στη συνέχεια στα αριστερά του σημείου Χ 1 η συνάρτηση αυξάνεται και μειώνεται στα δεξιά, επομένως, όταν Χ = Χ 1 συνάρτηση πηγαίνει από αύξουσα σε φθίνουσα, δηλαδή έχει μέγιστο.
Ομοίως, μπορούμε να εξετάσουμε σημεία Χ 2 και Χ 3 .

Όλα τα παραπάνω μπορούν να απεικονιστούν σχηματικά στην εικόνα:
Κανόνας για τη μελέτη της συνάρτησης y=f(x) για ακρότατο
Παραδείγματα. Εξερευνήστε λειτουργίες για το ελάχιστο και το μέγιστο.
ΜΕΓΙΣΤΕΣ ΚΑΙ ΜΙΚΡΟΤΕΡΕΣ ΤΙΜΕΣ ΜΙΑΣ ΣΥΝΑΡΤΗΣΗΣ ΣΕ ΕΝΑ Τμήμα
Το μεγαλύτεροη τιμή μιας συνάρτησης σε ένα διάστημα είναι η μεγαλύτερη από όλες τις τιμές της σε αυτό το διάστημα και το μικρότερο– η μικρότερη από όλες τις αξίες της.
Εξετάστε τη συνάρτηση y=f(x)συνεχής στο τμήμα [ α, β]. Όπως είναι γνωστό, μια τέτοια συνάρτηση φτάνει τις μέγιστες και τις ελάχιστες τιμές της, είτε στο όριο του τμήματος είτε μέσα σε αυτό. Εάν η μεγαλύτερη ή η μικρότερη τιμή μιας συνάρτησης επιτυγχάνεται σε ένα εσωτερικό σημείο του τμήματος, τότε αυτή η τιμή είναι το μέγιστο ή το ελάχιστο της συνάρτησης, δηλαδή επιτυγχάνεται σε κρίσιμα σημεία.
Έτσι, παίρνουμε το εξής κανόνας για την εύρεση της μεγαλύτερης και της μικρότερης τιμής μιας συνάρτησης σε ένα τμήμα[ α, β] :
Αφήστε τη συνάρτηση $z=f(x,y)$ να οριστεί σε κάποια γειτονιά του σημείου $(x_0,y_0)$. Λένε ότι το $(x_0,y_0)$ είναι ένα (τοπικό) μέγιστο σημείο εάν για όλα τα σημεία $(x,y)$ σε κάποια γειτονιά του σημείου $(x_0,y_0)$ η ανισότητα $f(x,y) είναι ικανοποιημένος< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, τότε το σημείο $(x_0,y_0)$ ονομάζεται το (τοπικό) ελάχιστο σημείο.
Τα μέγιστα και ελάχιστα σημεία ονομάζονται συχνά γενικός όρος - ακραία σημεία.
Εάν το $(x_0,y_0)$ είναι ένα μέγιστο σημείο, τότε η τιμή της συνάρτησης $f(x_0,y_0)$ σε αυτό το σημείο ονομάζεται μέγιστο της συνάρτησης $z=f(x,y)$. Αντίστοιχα, η τιμή της συνάρτησης στο ελάχιστο σημείο ονομάζεται ελάχιστη της συνάρτησης $z=f(x,y)$. Τα ελάχιστα και τα μέγιστα μιας συνάρτησης ενώνονται με έναν κοινό όρο - άκρα μιας συνάρτησης.
Αλγόριθμος για τη μελέτη της συνάρτησης $z=f(x,y)$ για ακρότατο
- Βρείτε τις μερικές παραγώγους $\frac(\μερικό z)(\μερικό x)$ και $\frac(\μερικό z)(\μερικό y)$. Να συνθέσετε και να λύσετε το σύστημα εξισώσεων $ \αριστερά \( \αρχή(ευθυγραμμισμένο) & \frac(\μερικό z)(\μερικό x)=0;\\ & \frac(\μερικό z)(\μερικό y)=0 \ end(aligned) \right.$ Τα σημεία των οποίων οι συντεταγμένες ικανοποιούν το καθορισμένο σύστημα ονομάζονται σταθερά.
- Βρείτε $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ και υπολογίστε την τιμή του $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ σε κάθε ακίνητο σημείο. Μετά από αυτό, χρησιμοποιήστε το ακόλουθο σχήμα:
- Αν $\Delta > 0$ και $\frac(\partial^2z)(\partial x^2) > 0$ (ή $\frac(\partial^2z)(\partial y^2) > 0$), τότε το υπό μελέτη σημείο είναι το ελάχιστο σημείο.
- Αν $\Delta > 0$ και $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Αν $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
- Εάν $\Delta = 0$, τότε δεν μπορεί να ειπωθεί τίποτα συγκεκριμένο για την παρουσία ενός ακραίου. απαιτείται πρόσθετη έρευνα.
Σημείωση (επιθυμητή για πληρέστερη κατανόηση του κειμένου): εμφάνιση/απόκρυψη
Αν $\Delta > 0$, τότε $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\ μερική^2z)(\μερική x\μερική y) \δεξιά)^2 > 0$. Και έπεται ότι $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) ( \μερικό x\μερικό y)\δεξιά)^2 ≥ 0$. Εκείνοι. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Αν το γινόμενο ορισμένων ποσοτήτων είναι μεγαλύτερο από το μηδέν, τότε αυτές οι ποσότητες έχουν το ίδιο πρόσημο. Δηλαδή, για παράδειγμα, αν $\frac(\partial^2z)(\partial x^2) > 0$, τότε $\frac(\partial^2z)(\partial y^2) > 0$. Εν ολίγοις, αν $\Delta > 0$ τότε τα πρόσημα των $\frac(\partial^2z)(\partial x^2)$ και $\frac(\partial^2z)(\partial y^2)$ συμπίπτουν .
Παράδειγμα Νο. 1
Εξετάστε τη συνάρτηση $z=4x^2-6xy-34x+5y^2+42y+7$ για το άκρο της.
$$ \frac(\μερικό z)(\μερικό x)=8x-6y-34; \frac(\μερικό z)(\μερικό y)=-6x+10y+42. $$
$$ \αριστερά \( \begin(στοιχισμένη) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(στοίχιση) \δεξιά. $$
Ας μειώσουμε κάθε εξίσωση αυτού του συστήματος κατά $2$ και ας μετακινήσουμε τους αριθμούς στις δεξιές πλευρές των εξισώσεων:
$$ \αριστερά \( \αρχή(στοίχιση) & 4x-3y=17;\\ & -3x+5y=-21. \end(στοίχιση) \δεξιά. $$
Αποκτήσαμε ένα σύστημα γραμμικών αλγεβρικών εξισώσεων. Σε αυτήν την κατάσταση, μου φαίνεται πιο βολικό να χρησιμοποιήσω τη μέθοδο Cramer για να λύσω το προκύπτον σύστημα.
$$ \begin(στοίχιση) & \Delta=\αριστερά| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\αριστερά| \begin(array) (cc) 17 & -3\\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\αριστερά| \begin(array) (cc) 4 & 17\\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(ευθυγραμμισμένο) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$
Οι τιμές $x=2$, $y=-3$ είναι οι συντεταγμένες του ακίνητου σημείου $(2;-3)$.
$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\μερική^2 z)(\μερική x \μερική y)=-6. $$
Ας υπολογίσουμε την τιμή του $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \μερική x\μερική y) \δεξιά)^2= 8\cdot 10-(-6)^2=80-36=44. $$
Εφόσον $\Delta > 0$ και $\frac(\partial^2 z)(\partial x^2) > 0$, τότε σύμφωνα με το σημείο $(2;-3)$ είναι το ελάχιστο σημείο της συνάρτησης $ z$. Βρίσκουμε το ελάχιστο της συνάρτησης $z$ αντικαθιστώντας τις συντεταγμένες του σημείου $(2;-3)$ στη δεδομένη συνάρτηση:
$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$
Απάντηση: $(2;-3)$ - ελάχιστος βαθμός; $z_(min)=-90$.
Παράδειγμα Νο. 2
Εξετάστε τη συνάρτηση $z=x^3+3xy^2-15x-12y+1$ για το άκρο της.
Θα ακολουθήσουμε τα παραπάνω. Αρχικά, ας βρούμε τις μερικές παραγώγους πρώτης τάξης:
$$ \frac(\μερικό z)(\μερικό x)=3x^2+3y^2-15; \frac(\μερικό z)(\μερικό y)=6xy-12. $$
Ας δημιουργήσουμε ένα σύστημα εξισώσεων $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( στοίχιση) \right.$:
$$ \αριστερά \( \begin(στοίχιση) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(στοίχιση) \δεξιά. $$
Ας μειώσουμε την πρώτη εξίσωση κατά 3 και τη δεύτερη κατά 6.
$$ \αριστερά \( \begin(στοίχιση) & x^2+y^2-5=0;\\ & xy-2=0. \end(στοίχιση) \δεξιά. $$
Αν $x=0$, τότε η δεύτερη εξίσωση θα μας οδηγήσει σε μια αντίφαση: $0\cdot y-2=0$, $-2=0$. Εξ ου και το συμπέρασμα: $x\neq 0$. Τότε από τη δεύτερη εξίσωση έχουμε: $xy=2$, $y=\frac(2)(x)$. Αντικαθιστώντας το $y=\frac(2)(x)$ στην πρώτη εξίσωση, θα έχουμε:
$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$
Πήραμε μια διτετραγωνική εξίσωση. Κάνουμε την αντικατάσταση $t=x^2$ (που σημαίνει ότι $t > 0$):
$$ t^2-5t+4=0;\\ \αρχή(στοίχιση) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(ευθυγραμμισμένο) $$
Αν $t=1$, τότε $x^2=1$. Ως εκ τούτου, έχουμε δύο τιμές $x$: $x_1=1$, $x_2=-1$. Αν $t=4$, τότε $x^2=4$, δηλ. $x_3=2$, $x_4=-2$. Αν θυμηθούμε ότι $y=\frac(2)(x)$, παίρνουμε:
\begin(ευθυγραμμισμένο) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2)=-1. \end (ευθυγραμμισμένο)
Έτσι, έχουμε τέσσερα ακίνητα σημεία: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Αυτό ολοκληρώνει το πρώτο βήμα του αλγορίθμου.
Τώρα ας ξεκινήσουμε με τον αλγόριθμο. Ας βρούμε τις μερικές παραγώγους δεύτερης τάξης:
$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\μερική^2 z)(\μερική x \μερική y)=6y. $$
Ας βρούμε $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \μερική x\μερική y) \δεξιά)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$
Τώρα θα υπολογίσουμε την τιμή του $\Delta$ σε καθένα από τα ακίνητα σημεία που βρέθηκαν προηγουμένως. Ας ξεκινήσουμε από το σημείο $M_1(1;2)$. Σε αυτό το σημείο έχουμε: $\Delta(M_1)=36(1^2-2^2)=-108$. Από $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.
Ας εξετάσουμε το σημείο $M_2(-1;-2)$. Σε αυτό το σημείο έχουμε: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Από $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.
Ας εξετάσουμε το σημείο $M_3(2;1)$. Σε αυτό το σημείο παίρνουμε:
$$ \Δέλτα(M_3)=36(2^2-1^2)=108;\;\; \αριστερά.\frac(\μερική^2 z)(\μερική x^2)\δεξιά|_(M_3)=6\cdot 2=12. $$
Αφού $\Delta(M_3) > 0$ και $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, τότε σύμφωνα με το $M_3(2; 1)$ είναι το ελάχιστο σημείο της συνάρτησης $z$. Βρίσκουμε το ελάχιστο της συνάρτησης $z$ αντικαθιστώντας τις συντεταγμένες του σημείου $M_3$ στη δεδομένη συνάρτηση:
$$ z_(min)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$
Απομένει να εξερευνήσουμε το σημείο $M_4(-2;-1)$. Σε αυτό το σημείο παίρνουμε:
$$ \Δέλτα(M_4)=36((-2)^2-(-1)^2)=108;\;\; \αριστερά.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$
Αφού $\Delta(M_4) > 0$ και $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$
Η ακραία μελέτη ολοκληρώθηκε. Το μόνο που μένει είναι να γράψουμε την απάντηση.
Απάντηση:
- $(2;1)$ - ελάχιστος πόντος, $z_(min)=-27$;
- $(-2;-1)$ - μέγιστος βαθμός, $z_(max)=29$.
Σημείωση
Στη γενική περίπτωση, δεν χρειάζεται να υπολογίσουμε την τιμή του $\Delta$, γιατί μας ενδιαφέρει μόνο το πρόσημο και όχι η συγκεκριμένη τιμή αυτής της παραμέτρου. Για παράδειγμα, για παράδειγμα το Νο. 2 που εξετάστηκε παραπάνω, στο σημείο $M_3(2;1)$ έχουμε $\Delta=36\cdot(2^2-1^2)$. Εδώ είναι προφανές ότι $\Delta > 0$ (καθώς και οι δύο παράγοντες $36$ και $(2^2-1^2)$ είναι θετικοί) και είναι δυνατόν να μην βρεθεί μια συγκεκριμένη τιμή $\Delta$. Είναι αλήθεια ότι για τυπικούς υπολογισμούς αυτή η παρατήρηση είναι άχρηστη - εκεί σας ζητούν να φέρετε τους υπολογισμούς σε έναν αριθμό :)
Παράδειγμα Νο. 3
Εξετάστε τη συνάρτηση $z=x^4+y^4-2x^2+4xy-2y^2+3$ για το άκρο της.
Θα ακολουθήσουμε. Αρχικά, ας βρούμε τις μερικές παραγώγους πρώτης τάξης:
$$ \frac(\μερικό z)(\μερικό x)=4x^3-4x+4y; \frac(\μερικό z)(\μερικό y)=4y^3+4x-4y. $$
Ας δημιουργήσουμε ένα σύστημα εξισώσεων $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( στοίχιση) \right.$:
$$ \αριστερά \( \αρχή(στοίχιση) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(στοίχιση) \δεξιά. $$
Ας μειώσουμε και τις δύο εξισώσεις κατά $4$:
$$ \αριστερά \( \αρχή(στοίχιση) & x^3-x+y=0;\\ & y^3+x-y=0. \end(στοίχιση) \δεξιά. $$
Ας προσθέσουμε την πρώτη εξίσωση στη δεύτερη και ας εκφράσουμε το $y$ ως $x$:
$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$
Αντικαθιστώντας το $y=-x$ στην πρώτη εξίσωση του συστήματος, θα έχουμε:
$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$
Από την εξίσωση που προκύπτει έχουμε: $x=0$ ή $x^2-2=0$. Από την εξίσωση $x^2-2=0$ προκύπτει ότι $x=-\sqrt(2)$ ή $x=\sqrt(2)$. Έτσι, βρέθηκαν τρεις τιμές των $x$, δηλαδή: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Από $y=-x$, τότε $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.
Το πρώτο βήμα της λύσης έχει ολοκληρωθεί. Πήραμε τρία σταθερά σημεία: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .
Τώρα ας ξεκινήσουμε με τον αλγόριθμο. Ας βρούμε τις μερικές παραγώγους δεύτερης τάξης:
$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\μερική^2 z)(\μερική x \μερική y)=4. $$
Ας βρούμε $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \μερικό x\μερικό y) \δεξιά)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$
Τώρα θα υπολογίσουμε την τιμή του $\Delta$ σε καθένα από τα ακίνητα σημεία που βρέθηκαν προηγουμένως. Ας ξεκινήσουμε από το σημείο $M_1(0;0)$. Σε αυτό το σημείο έχουμε: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Εφόσον $\Delta(M_1) = 0$, τότε απαιτείται πρόσθετη έρευνα, καθώς δεν μπορεί να ειπωθεί τίποτα συγκεκριμένο για την παρουσία ενός ακραίου στο υπό εξέταση σημείο. Ας αφήσουμε προς το παρόν αυτό το σημείο και ας προχωρήσουμε σε άλλα σημεία.
Ας εξετάσουμε το σημείο $M_2(-\sqrt(2),\sqrt(2))$. Σε αυτό το σημείο παίρνουμε:
\begin(aligned) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \αριστερά.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end (ευθυγραμμισμένο)
Αφού $\Delta(M_2) > 0$ and $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, τότε σύμφωνα με το $M_2(-\ sqrt(2),\sqrt(2))$ είναι το ελάχιστο σημείο της συνάρτησης $z$. Βρίσκουμε το ελάχιστο της συνάρτησης $z$ αντικαθιστώντας τις συντεταγμένες του σημείου $M_2$ στη δεδομένη συνάρτηση:
$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$
Ομοίως με το προηγούμενο σημείο, εξετάζουμε το σημείο $M_3(\sqrt(2),-\sqrt(2))$. Σε αυτό το σημείο παίρνουμε:
\begin(aligned) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \αριστερά.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end (ευθυγραμμισμένο)
Αφού $\Delta(M_3) > 0$ and $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, τότε σύμφωνα με το $M_3(\sqrt (2),-\sqrt(2))$ είναι το ελάχιστο σημείο της συνάρτησης $z$. Βρίσκουμε το ελάχιστο της συνάρτησης $z$ αντικαθιστώντας τις συντεταγμένες του σημείου $M_3$ στη δεδομένη συνάρτηση:
$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2 ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$
Ήρθε η ώρα να επιστρέψετε στο σημείο $M_1(0;0)$, στο οποίο $\Delta(M_1) = 0$. Σύμφωνα με αυτό, απαιτείται πρόσθετη έρευνα. Αυτή η υπεκφυγή φράση σημαίνει "κάνε αυτό που θέλεις" :). Δεν υπάρχει γενικός τρόπος επίλυσης τέτοιων καταστάσεων, και αυτό είναι κατανοητό. Αν υπήρχε μια τέτοια μέθοδος, θα είχε συμπεριληφθεί σε όλα τα σχολικά βιβλία εδώ και πολύ καιρό. Στο μεταξύ, πρέπει να αναζητήσουμε μια ειδική προσέγγιση σε κάθε σημείο στο οποίο $\Delta = 0$. Λοιπόν, ας εξετάσουμε τη συμπεριφορά της συνάρτησης κοντά στο σημείο $M_1(0;0)$. Ας σημειώσουμε αμέσως ότι $z(M_1)=z(0;0)=3$. Ας υποθέσουμε ότι το $M_1(0;0)$ είναι το ελάχιστο σημείο. Τότε για οποιοδήποτε σημείο $M$ από κάποια γειτονιά του σημείου $M_1(0;0)$ λαμβάνουμε $z(M) > z(M_1)$, δηλ. $z(M) > 3$. Τι γίνεται αν κάποια γειτονιά περιέχει σημεία στα οποία $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Ας εξετάσουμε σημεία για τα οποία $y=0$, π.χ. σημεία της μορφής $(x,0)$. Σε αυτά τα σημεία η συνάρτηση $z$ θα λάβει τις ακόλουθες τιμές:
$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$
Σε όλες τις αρκετά μικρές γειτονιές $M_1(0;0)$ έχουμε $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Αλλά ίσως το σημείο $M_1(0;0)$ είναι το μέγιστο σημείο; Εάν ισχύει αυτό, τότε για οποιοδήποτε σημείο $M$ από κάποια γειτονιά του σημείου $M_1(0;0)$ λαμβάνουμε $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3$? Τότε σίγουρα δεν θα υπάρχει μέγιστο στο σημείο $M_1$.
Ας εξετάσουμε σημεία για τα οποία $y=x$, π.χ. σημεία της μορφής $(x,x)$. Σε αυτά τα σημεία η συνάρτηση $z$ θα λάβει τις ακόλουθες τιμές:
$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$
Εφόσον σε οποιαδήποτε γειτονιά του σημείου $M_1(0;0)$ έχουμε $2x^4 > 0$, μετά $2x^4+3 > 3$. Συμπέρασμα: οποιαδήποτε γειτονιά του σημείου $M_1(0;0)$ περιέχει σημεία στα οποία $z > 3$, επομένως το σημείο $M_1(0;0)$ δεν μπορεί να είναι μέγιστο σημείο.
Το σημείο $M_1(0;0)$ δεν είναι ούτε μέγιστο ούτε ελάχιστο σημείο. Συμπέρασμα: Το $M_1$ δεν είναι καθόλου ακραίο σημείο.
Απάντηση: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ είναι τα ελάχιστα σημεία της συνάρτησης $z$. Και στα δύο σημεία $z_(min)=-5$.
Καλείται το σημείο x 0 μέγιστο σημείο(ελάχιστο) συνάρτηση f(x), εάν σε κάποια γειτονιά του σημείου x 0 η ανίσωση f(x) ≤f(x 0) (f(x) ≥f(x 0)) ικανοποιείται.
Η τιμή της συνάρτησης σε αυτό το σημείο καλείται ανάλογα ανώτατο όριοή ελάχιστολειτουργίες. Η μέγιστη και η ελάχιστη συνάρτηση ενώνονται με ένα κοινό όνομα ακραίολειτουργίες.
Το άκρο μιας συνάρτησης με αυτή την έννοια ονομάζεται συχνά τοπικό εξτρέμ, τονίζοντας το γεγονός ότι αυτή η έννοια συνδέεται μόνο με μια αρκετά μικρή γειτονιά του σημείου x 0. Στο ίδιο διάστημα, μια συνάρτηση μπορεί να έχει πολλά τοπικά μέγιστα και ελάχιστα, τα οποία δεν συμπίπτουν απαραίτητα με παγκόσμιο μέγιστοή ελάχιστο(δηλαδή η μεγαλύτερη ή η μικρότερη τιμή της συνάρτησης σε ολόκληρο το διάστημα).
Απαραίτητη προϋπόθεση για εξτρέμ. Για να έχει μια συνάρτηση ακρότατο σε ένα σημείο, είναι απαραίτητο η παράγωγός της σε αυτό το σημείο να είναι ίση με το μηδέν ή να μην υπάρχει.
Για διαφοροποιήσιμες συναρτήσεις, αυτή η συνθήκη προκύπτει από το θεώρημα του Fermat. Επιπλέον, προβλέπει επίσης την περίπτωση που μια συνάρτηση έχει ένα άκρο σε σημείο στο οποίο δεν είναι διαφοροποιήσιμο.
Τα σημεία στα οποία ικανοποιείται η απαραίτητη ακραία συνθήκη ονομάζονται κρίσιμος(ή ακίνητοςγια μια διαφοροποιήσιμη συνάρτηση). Αυτά τα σημεία πρέπει να βρίσκονται εντός του τομέα της συνάρτησης.
Έτσι, εάν υπάρχει ακρότατο σε οποιοδήποτε σημείο, τότε αυτό το σημείο είναι κρίσιμο (απαραίτητη συνθήκη). Σημειώστε ότι το αντίστροφο δεν ισχύει. Το κρίσιμο σημείο δεν είναι απαραίτητα ένα ακραίο σημείο, δηλ. η αναφερόμενη προϋπόθεση δεν είναι επαρκής.
Η πρώτη επαρκής προϋπόθεση για ένα εξτρέμ. Εάν, όταν διέρχεται από ένα ορισμένο σημείο, η παράγωγος της διαφοροποιήσιμης συνάρτησης αλλάζει πρόσημο από συν σε μείον, τότε αυτό είναι το μέγιστο σημείο της συνάρτησης και αν από μείον στο συν, τότε αυτό είναι το ελάχιστο σημείο.
Η απόδειξη αυτής της συνθήκης προκύπτει από την επαρκή συνθήκη της μονοτονίας (όταν αλλάζει το πρόσημο της παραγώγου, γίνεται μετάβαση είτε από αύξηση της συνάρτησης σε μείωση, είτε από μείωση σε αύξηση).
Η δεύτερη επαρκής προϋπόθεση για ένα ακραίο. Εάν η πρώτη παράγωγος μιας δύο φορές διαφοροποιήσιμης συνάρτησης σε κάποιο σημείο είναι μηδέν και η δεύτερη παράγωγος σε αυτό το σημείο είναι θετική, τότε αυτό είναι το ελάχιστο σημείο της συνάρτησης. και αν η δεύτερη παράγωγος είναι αρνητική, τότε αυτό είναι το μέγιστο σημείο.
Η απόδειξη αυτής της συνθήκης βασίζεται και στην επαρκή συνθήκη της μονοτονίας. Στην πραγματικότητα, εάν η δεύτερη παράγωγος είναι θετική, τότε η πρώτη παράγωγος είναι αύξουσα συνάρτηση. Εφόσον στο επίμαχο σημείο είναι ίσο με μηδέν, επομένως, όταν το περνάει, αλλάζει πρόσημο από μείον σε συν, γεγονός που μας επιστρέφει στην πρώτη επαρκή συνθήκη για ένα τοπικό ελάχιστο. Ομοίως, εάν η δεύτερη παράγωγος είναι αρνητική, τότε η πρώτη μειώνεται και αλλάζει πρόσημο από συν σε πλην, που είναι επαρκής συνθήκη για ένα τοπικό μέγιστο.
Μελέτη συνάρτησης για ακραίοσύμφωνα με τα διατυπωμένα θεωρήματα, περιλαμβάνει τα ακόλουθα στάδια:
1. Να βρείτε την πρώτη παράγωγο της συνάρτησης f`(x).
2. Ελέγξτε την εκπλήρωση της απαραίτητης ακραίας συνθήκης, π.χ. βρείτε τα κρίσιμα σημεία της συνάρτησης f(x) στα οποία η παράγωγος f`(x) = 0 ή δεν υπάρχει.
3. Ελέγξτε ότι πληρούται η επαρκής προϋπόθεση για το ακραίο, π.χ. είτε εξετάστε το πρόσημο της παραγώγου αριστερά και δεξιά κάθε κρίσιμου σημείου, είτε βρείτε τη δεύτερη παράγωγο f``(x) και προσδιορίστε το πρόσημό της σε κάθε κρίσιμο σημείο. Εξάγετε ένα συμπέρασμα σχετικά με την παρουσία των ακραίων της συνάρτησης.
4. Βρείτε τα άκρα (ακραίες τιμές) της συνάρτησης.
Εύρεση του καθολικού μέγιστου και ελάχιστου μιας συνάρτησηςγια ένα ορισμένο χρονικό διάστημα έχει επίσης μεγάλη πρακτική σημασία. Η λύση σε αυτό το πρόβλημα σε ένα τμήμα βασίζεται στο θεώρημα του Weierstrass, σύμφωνα με το οποίο μια συνεχής συνάρτηση παίρνει τις μεγαλύτερες και τις μικρότερες τιμές της σε ένα τμήμα. Μπορούν να επιτευχθούν τόσο σε ακραία σημεία όσο και στα άκρα του τμήματος. Επομένως, η λύση περιλαμβάνει τα ακόλουθα βήματα:
1. Να βρείτε την παράγωγο της συνάρτησης f`(x).
2. Να βρείτε τα κρίσιμα σημεία της συνάρτησης f(x), στα οποία η παράγωγος f`(x) = 0 ή δεν υπάρχει.
3. Βρείτε τις τιμές της συνάρτησης σε κρίσιμα σημεία και στα άκρα του τμήματος και επιλέξτε τη μεγαλύτερη και τη μικρότερη από αυτές.
Αυτή είναι μια αρκετά ενδιαφέρουσα ενότητα των μαθηματικών, την οποία αντιμετωπίζουν όλοι οι απόφοιτοι και οι φοιτητές. Ωστόσο, δεν αρέσει σε όλους το matan. Μερικοί δεν μπορούν να κατανοήσουν ακόμη και βασικά πράγματα, όπως μια φαινομενικά τυπική μελέτη συναρτήσεων. Αυτό το άρθρο έχει σκοπό να διορθώσει μια τέτοια παράβλεψη. Θέλετε να μάθετε περισσότερα σχετικά με την ανάλυση συνάρτησης; Θα θέλατε να μάθετε τι είναι τα ακραία σημεία και πώς να τα βρείτε; Τότε αυτό το άρθρο είναι για εσάς.
Μελετώντας τη γραφική παράσταση μιας συνάρτησης
Πρώτον, αξίζει να καταλάβετε γιατί πρέπει να αναλύσετε καθόλου το γράφημα. Υπάρχουν απλές συναρτήσεις που δεν είναι δύσκολο να σχεδιαστούν. Ένα εντυπωσιακό παράδειγμα μιας τέτοιας συνάρτησης είναι η παραβολή. Δεν θα είναι δύσκολο να σχεδιάσετε ένα γράφημα. Το μόνο που χρειάζεται είναι, χρησιμοποιώντας έναν απλό μετασχηματισμό, να βρείτε τους αριθμούς στους οποίους η συνάρτηση παίρνει την τιμή 0. Και καταρχήν, αυτό είναι το μόνο που χρειάζεται να γνωρίζετε για να σχεδιάσετε ένα γράφημα μιας παραβολής.
Τι γίνεται όμως αν η συνάρτηση που πρέπει να γράψουμε είναι πολύ πιο περίπλοκη; Δεδομένου ότι οι ιδιότητες των σύνθετων συναρτήσεων δεν είναι αρκετά προφανείς, είναι απαραίτητο να πραγματοποιηθεί μια ολόκληρη ανάλυση. Μόνο μετά από αυτό μπορεί η λειτουργία να απεικονιστεί γραφικά. Πώς να το κάνετε αυτό; Μπορείτε να βρείτε την απάντηση σε αυτήν την ερώτηση σε αυτό το άρθρο.
Σχέδιο Ανάλυσης Συναρτήσεων
Το πρώτο πράγμα που πρέπει να κάνουμε είναι να κάνουμε μια επιφανειακή μελέτη της συνάρτησης, κατά την οποία βρίσκουμε το πεδίο ορισμού. Λοιπόν, ας ξεκινήσουμε με τη σειρά. Ο τομέας ορισμού είναι το σύνολο των τιμών με το οποίο ορίζεται η συνάρτηση. Με απλά λόγια, αυτοί είναι οι αριθμοί που μπορούν να χρησιμοποιηθούν σε μια συνάρτηση αντί για x. Για να προσδιορίσετε το εύρος, πρέπει απλώς να δείτε την εγγραφή. Για παράδειγμα, είναι προφανές ότι η συνάρτηση y (x) = x 3 + x 2 - x + 43 έχει ένα πεδίο ορισμού που είναι το σύνολο των πραγματικών αριθμών. Λοιπόν, με μια συνάρτηση όπως (x 2 - 2x)/x όλα είναι λίγο διαφορετικά. Εφόσον ο αριθμός στον παρονομαστή δεν πρέπει να είναι ίσος με 0, το πεδίο ορισμού αυτής της συνάρτησης θα είναι όλοι οι πραγματικοί αριθμοί εκτός από το μηδέν.
Στη συνέχεια, πρέπει να βρείτε τα λεγόμενα μηδενικά της συνάρτησης. Αυτές είναι οι τιμές ορίσματος στις οποίες ολόκληρη η συνάρτηση παίρνει την τιμή μηδέν. Για να γίνει αυτό, είναι απαραίτητο να εξισώσετε τη συνάρτηση με το μηδέν, να την εξετάσετε λεπτομερώς και να εκτελέσετε ορισμένους μετασχηματισμούς. Ας πάρουμε την ήδη γνωστή συνάρτηση y(x) = (x 2 - 2x)/x. Από το σχολικό μάθημα γνωρίζουμε ότι ένα κλάσμα είναι ίσο με 0 όταν ο αριθμητής είναι ίσος με μηδέν. Επομένως, απορρίπτουμε τον παρονομαστή και αρχίζουμε να εργαζόμαστε με τον αριθμητή, εξισώνοντάς τον με μηδέν. Παίρνουμε x 2 - 2x = 0 και βάζουμε x εκτός παρενθέσεων. Άρα x (x - 2) = 0. Ως αποτέλεσμα, βρίσκουμε ότι η συνάρτησή μας είναι ίση με μηδέν όταν το x είναι 0 ή 2.
Κατά τη μελέτη του γραφήματος μιας συνάρτησης, πολλοί άνθρωποι αντιμετωπίζουν προβλήματα με τη μορφή ακραίων σημείων. Και είναι περίεργο. Εξάλλου, τα άκρα είναι ένα αρκετά απλό θέμα. Δεν με πιστεύεις; Δείτε μόνοι σας διαβάζοντας αυτό το μέρος του άρθρου, στο οποίο θα μιλήσουμε για ελάχιστους και μέγιστους βαθμούς.

Πρώτον, αξίζει να καταλάβουμε τι είναι ακραίο. Ένα άκρο είναι η οριακή τιμή που φτάνει μια συνάρτηση σε ένα γράφημα. Αποδεικνύεται ότι υπάρχουν δύο ακραίες τιμές - μέγιστη και ελάχιστη. Για σαφήνεια, μπορείτε να δείτε την παραπάνω εικόνα. Στην περιοχή που μελετήθηκε, το σημείο -1 είναι το μέγιστο της συνάρτησης y (x) = x 5 - 5x, και το σημείο 1, αντίστοιχα, είναι το ελάχιστο.
Επίσης, μην μπερδεύετε τις έννοιες. Τα ακραία σημεία μιας συνάρτησης είναι εκείνα τα ορίσματα στα οποία μια δεδομένη συνάρτηση αποκτά ακραίες τιμές. Με τη σειρά του, το άκρο είναι η τιμή των ελαχίστων και μεγίστων μιας συνάρτησης. Για παράδειγμα, εξετάστε ξανά το παραπάνω σχήμα. -1 και 1 είναι τα ακρότατα σημεία της συνάρτησης και τα 4 και -4 είναι τα ίδια τα άκρα.
Εύρεση ακραίων σημείων

Πώς όμως βρίσκετε τα ακραία σημεία μιας συνάρτησης; Όλα είναι αρκετά απλά. Το πρώτο πράγμα που πρέπει να κάνετε είναι να βρείτε την παράγωγο της εξίσωσης. Ας πούμε ότι λάβαμε την εργασία: «Βρείτε τα ακραία σημεία της συνάρτησης y (x), x είναι το όρισμα για λόγους σαφήνειας, ας πάρουμε τη συνάρτηση y (x) = x 3 + 2x 2 + x + 54. Ας διαφοροποιήσουμε και. πάρτε την ακόλουθη εξίσωση: 3x 2 + 4x + 1. Ως αποτέλεσμα, έχουμε μια τυπική τετραγωνική εξίσωση το μόνο που χρειάζεται να κάνουμε είναι να την εξισώσουμε με το μηδέν και να βρούμε τις ρίζες (Δ = 16 - 12 = 4), αυτή η εξίσωση καθορίζεται από δύο ρίζες και τις παίρνουμε: 1/3 και -1 είναι ποιο σημείο είναι το μέγιστο και ποιο το ελάχιστο, πρέπει να πάρετε το γειτονικό σημείο και να λάβετε τον αριθμό -2, που βρίσκεται στα αριστερά κατά μήκος της γραμμής συντεταγμένων; 1. Αντικαταστήστε αυτή την τιμή στην εξίσωσή μας y(-2) = 12 - 8 + 1 = 5. Ως αποτέλεσμα, παίρνουμε έναν θετικό αριθμό Αυτό σημαίνει ότι στο διάστημα από 1/3 έως -1 η συνάρτηση αυξάνεται. Αυτό, με τη σειρά του, σημαίνει ότι στα διαστήματα από μείον άπειρο έως 1/3 και από -1 έως συν άπειρο η συνάρτηση μειώνεται. Έτσι, μπορούμε να συμπεράνουμε ότι ο αριθμός 1/3 είναι το ελάχιστο σημείο της συνάρτησης στο διάστημα που μελετήθηκε και -1 είναι το μέγιστο σημείο.

Αξίζει επίσης να σημειωθεί ότι η Ενιαία Κρατική Εξέταση απαιτεί όχι μόνο την εύρεση ακραίων σημείων, αλλά και την εκτέλεση κάποιου είδους λειτουργίας με αυτούς (προσθήκη, πολλαπλασιασμό κ.λπ.). Για αυτό το λόγο αξίζει να δοθεί ιδιαίτερη προσοχή στις συνθήκες του προβλήματος. Εξάλλου, λόγω απροσεξίας, μπορεί να χάσεις πόντους.




