Finden und untersuchen Sie die Extrempunkte der Funktion. Das zweite Zeichen eines Extremums einer Funktion
Einführung
In vielen Bereichen der Wissenschaft und der Praxis steht man oft vor dem Problem, das Extremum einer Funktion zu finden. Tatsache ist, dass viele technische, wirtschaftliche usw. Prozesse werden durch eine Funktion oder mehrere Funktionen modelliert, die von Variablen abhängen – Faktoren, die den Zustand des modellierten Phänomens beeinflussen. Um die optimale (rationale) Zustands- und Prozesssteuerung zu ermitteln, ist es erforderlich, die Extrema solcher Funktionen zu finden. So werden in den Wirtschaftswissenschaften oft die Probleme der Kostenminimierung oder Gewinnmaximierung gelöst – das mikroökonomische Problem des Unternehmens. In dieser Arbeit betrachten wir keine Modellierungsprobleme, sondern betrachten nur Algorithmen zur Suche nach Extrema von Funktionen in der einfachsten Version, wenn den Variablen keine Einschränkungen auferlegt werden (bedingungslose Optimierung) und das Extremum nur für eine Zielfunktion gesucht wird.
EXTREMA DER FUNKTION
Betrachten Sie den Graphen einer stetigen Funktion y=f(x) in der Abbildung dargestellt. Funktionswert an einem Punkt X 1 wird größer sein als die Funktionswerte an allen benachbarten Punkten sowohl links als auch rechts davon X 1 . In diesem Fall sagen wir, dass die Funktion den Punkt hat X Maximal 1. Am Punkt X Funktion 3 hat offensichtlich auch ein Maximum. Wenn wir den Punkt bedenken X 2, dann ist der darin enthaltene Funktionswert kleiner als alle benachbarten Werte. In diesem Fall sagen wir, dass die Funktion den Punkt hat X Mindestens 2. Ebenso für den Punkt X 4 .
Funktion y=f(x) am Punkt X 0 hat maximal, wenn der Wert der Funktion an diesem Punkt größer ist als ihre Werte an allen Punkten eines Intervalls, das den Punkt enthält X 0, d.h. wenn es eine solche Umgebung eines Punktes gibt X 0, was für alle gilt X≠X 0 , Zugehörigkeit zu dieser Nachbarschaft gilt die Ungleichung f(x)<f(x 0 ) .
Funktion y=f(x) Es hat Minimum am Punkt X 0 , wenn es eine solche Umgebung eines Punktes gibt X 0 , das ist für jeden etwas X≠X 0 zu dieser Nachbarschaft gehört, gilt die Ungleichung f(x)>f(x 0.
Die Punkte, an denen die Funktion ihr Maximum und Minimum erreicht, werden Extrempunkte genannt, und die Werte der Funktion an diesen Punkten werden Extrema der Funktion genannt.
Beachten wir die Tatsache, dass eine auf einem Segment definierte Funktion ihr Maximum und Minimum nur an Punkten erreichen kann, die innerhalb des betrachteten Segments liegen.
Beachten Sie, dass wenn eine Funktion an einem Punkt ein Maximum aufweist, dies nicht bedeutet, dass die Funktion an diesem Punkt den größten Wert im gesamten Definitionsbereich hat. In der oben besprochenen Abbildung ist die Funktion an dem Punkt X 1 hat ein Maximum, obwohl es Punkte gibt, an denen die Funktionswerte größer sind als am Punkt X 1 . Insbesondere, F(X 1) < F(X 4) d.h. Das Minimum einer Funktion ist größer als das Maximum. Aus der Definition des Maximums folgt lediglich, dass dies der größte Wert der Funktion an Punkten ist, die hinreichend nahe am Maximalpunkt liegen.
Satz 1. (Eine notwendige Bedingung für die Existenz eines Extremums.) Wenn die differenzierbare Funktion y=f(x) hat auf den Punkt x= x 0 Extremum, dann wird seine Ableitung an diesem Punkt Null.
Nachweisen. Lassen Sie uns der Sicherheit halber auf den Punkt kommen X 0-Funktion hat ein Maximum. Dann gilt für ausreichend kleine Inkremente Δ X wir haben f(x 0 + Δ X)
Übergabe dieser Ungleichungen an den Grenzwert bei Δ X→ 0 und unter Berücksichtigung der Ableitung F "(X 0) existiert, und daher hängt der Grenzwert links nicht davon ab, wie Δ X→ 0 erhalten wir: bei Δ X → 0 – 0 F"(X 0) ≥ 0 a bei Δ X → 0 + 0 F"(X 0) ≤ 0. Da F"(X 0) eine Zahl definiert, dann sind diese beiden Ungleichungen nur dann kompatibel, wenn F"(X 0) = 0.
Der bewährte Satz besagt, dass die Maximal- und Minimalpunkte nur zu den Werten des Arguments gehören können, bei denen die Ableitung Null wird.
Wir haben den Fall betrachtet, dass eine Funktion an allen Punkten eines bestimmten Segments eine Ableitung hat. Wie verhält es sich, wenn das Derivat nicht existiert? Schauen wir uns Beispiele an.
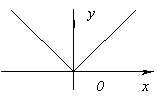
j=|X|.
Die Funktion hat an diesem Punkt keine Ableitung X=0 (an diesem Punkt hat der Graph der Funktion keinen definierten Tangens), aber an diesem Punkt hat die Funktion ein Minimum, da j(0)=0 und für alle X≠ 0j > 0.
hat keine Ableitung bei X=0, da es bei unendlich geht X=0. Aber an diesem Punkt hat die Funktion ein Maximum. hat keine Ableitung bei X=0, seit wann X→0. Zu diesem Zeitpunkt hat die Funktion weder ein Maximum noch ein Minimum. Wirklich, f(x)=0 und bei X<0f(x)<0, а при X>0f(x)>0.Aus den gegebenen Beispielen und dem formulierten Satz geht somit klar hervor, dass eine Funktion nur in zwei Fällen ein Extremum haben kann: 1) an Punkten, an denen die Ableitung existiert und gleich Null ist; 2) an dem Punkt, an dem die Ableitung nicht existiert.
Wenn jedoch irgendwann X 0 das wissen wir f "(x 0 ) =0, dann kann man hieraus nicht auf das schließen X 0 hat die Funktion ein Extremum.
Zum Beispiel.
.Aber Punkt X=0 ist kein Extrempunkt, da links von diesem Punkt die Funktionswerte unterhalb der Achse liegen Ochse, und rechts oben.
Es werden Werte eines Arguments aus dem Definitionsbereich einer Funktion aufgerufen, bei denen die Ableitung der Funktion verschwindet oder nicht existiert kritische Punkte.
Aus alledem folgt, dass die Extrempunkte der Funktion zu den kritischen Punkten gehören, allerdings ist nicht jeder kritische Punkt ein Extrempunkt. Um das Extremum einer Funktion zu ermitteln, müssen Sie daher alle kritischen Punkte der Funktion ermitteln und dann jeden dieser Punkte separat auf Maximum und Minimum untersuchen. Hierzu dient der folgende Satz.
Satz 2. (Eine hinreichende Bedingung für die Existenz eines Extremums.) Die Funktion sei in einem Intervall, das den kritischen Punkt enthält, stetig X 0 und ist an allen Punkten dieses Intervalls differenzierbar (außer vielleicht am Punkt selbst). X 0). Wenn bei der Bewegung von links nach rechts durch diesen Punkt die Ableitung das Vorzeichen von Plus nach Minus ändert, dann an diesem Punkt X = X 0-Funktion hat ein Maximum. Wenn, bei der Durchreise X 0 von links nach rechts ändert die Ableitung das Vorzeichen von Minus nach Plus, dann hat die Funktion an dieser Stelle ein Minimum.
Also, wenn
f "(x)>0 um X<X 0 und f "(x)< 0 um x>x 0 also X 0 – Höchstpunktzahl;
bei X<X 0 und f "(x)> 0 um x>x 0 also X 0 – Mindestpunktzahl.Nachweisen. Nehmen wir zunächst einmal an, dass es sich um eine Durchreise handelt X 0 ändert die Ableitung das Vorzeichen von Plus nach Minus, d.h. Vor allen X, nah am Punkt X 0 f "(x)> 0 für X< x 0 , f "(x)< 0 für x>x 0 . Wenden wir den Satz von Lagrange auf die Differenz an f(x) - f(x 0 ) = f "(c)(x- x 0), wo C liegt zwischen X Und X 0 .
Lassen X< x 0 . Dann C< x 0 und f "(c)> 0. Deshalb f "(c)(x- x 0)< 0 und daher
f(x) - f(x 0 )< 0, d.h. f(x)< f(x 0 ).
Lassen x > x 0 . Dann c>x 0 und f "(c)< 0. Bedeutet f "(c)(x- x 0)< 0. Deshalb f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
Also für alle Werte X nah genug dran X 0 f(x)< f(x 0 ) . Und das bedeutet auf den Punkt gebracht X 0-Funktion hat ein Maximum.
Der zweite Teil des Minimumsatzes wird auf ähnliche Weise bewiesen.
Lassen Sie uns die Bedeutung dieses Theorems in der Abbildung veranschaulichen. Lassen f "(x 1 ) =0 und für alle X, nah genug dran X 1 sind die Ungleichungen erfüllt
f "(x)< 0 um X< x 1 , f "(x)> 0 um x>x 1 .
Dann links vom Punkt X 1 Die Funktion nimmt rechts zu und ab, also wann X = X 1 Funktion geht von steigend nach fallend, das heißt, sie hat ein Maximum.
Ebenso können wir Punkte berücksichtigen X 2 und X 3 .
Alles oben Genannte kann im Bild schematisch dargestellt werden:
Regel zum Studieren der Funktion y=f(x) für Extremum
Finden Sie den Definitionsbereich einer Funktion f(x).
Finden Sie die erste Ableitung einer Funktion f "(x).
Bestimmen Sie hierfür kritische Punkte:
Finden Sie die wahren Wurzeln der Gleichung f "(x)=0;
Finden Sie alle Werte X für die die Ableitung f "(x) existiert nicht.
Bestimmen Sie das Vorzeichen der Ableitung links und rechts vom kritischen Punkt. Da das Vorzeichen der Ableitung zwischen zwei kritischen Punkten konstant bleibt, reicht es aus, das Vorzeichen der Ableitung an einem Punkt links und einem Punkt rechts vom kritischen Punkt zu bestimmen.
Berechnen Sie den Wert der Funktion an den Extrempunkten.
Betrachten Sie den Graphen einer stetigen Funktion y=f(x) in der Abbildung dargestellt.
Funktionswert an einem Punkt X 1 wird größer sein als die Funktionswerte an allen benachbarten Punkten sowohl links als auch rechts davon X 1 . In diesem Fall sagen wir, dass die Funktion den Punkt hat X Maximal 1. Am Punkt X Funktion 3 hat offensichtlich auch ein Maximum. Wenn wir den Punkt bedenken X 2, dann ist der darin enthaltene Funktionswert kleiner als alle benachbarten Werte. In diesem Fall sagen wir, dass die Funktion den Punkt hat X Mindestens 2. Ebenso für den Punkt X 4 .
Funktion y=f(x) am Punkt X 0 hat maximal, wenn der Wert der Funktion an diesem Punkt größer ist als ihre Werte an allen Punkten eines Intervalls, das den Punkt enthält X 0, d.h. wenn es eine solche Umgebung eines Punktes gibt X 0, was für alle gilt X≠X 0 , Zugehörigkeit zu dieser Nachbarschaft gilt die Ungleichung f(x)<f(x 0 ) .
Funktion y=f(x) Es hat Minimum am Punkt X 0 , wenn es eine solche Umgebung eines Punktes gibt X 0 , das ist für jeden etwas X≠X 0 zu dieser Nachbarschaft gehört, gilt die Ungleichung f(x)>f(x 0.
Die Punkte, an denen die Funktion ihr Maximum und Minimum erreicht, werden Extrempunkte genannt, und die Werte der Funktion an diesen Punkten werden Extrema der Funktion genannt.
Beachten wir die Tatsache, dass eine auf einem Segment definierte Funktion ihr Maximum und Minimum nur an Punkten erreichen kann, die innerhalb des betrachteten Segments liegen.
Beachten Sie, dass wenn eine Funktion an einem Punkt ein Maximum aufweist, dies nicht bedeutet, dass die Funktion an diesem Punkt den größten Wert im gesamten Definitionsbereich hat. In der oben besprochenen Abbildung ist die Funktion an dem Punkt X 1 hat ein Maximum, obwohl es Punkte gibt, an denen die Funktionswerte größer sind als am Punkt X 1 . Insbesondere, F(X 1) < F(X 4) d.h. Das Minimum einer Funktion ist größer als das Maximum. Aus der Definition des Maximums folgt lediglich, dass dies der größte Wert der Funktion an Punkten ist, die hinreichend nahe am Maximalpunkt liegen.
Satz 1. (Notwendige Bedingung für die Existenz eines Extremums.) Wenn die differenzierbare Funktion y=f(x) hat auf den Punkt x= x 0 Extremum, dann wird seine Ableitung an diesem Punkt Null.
Nachweisen. Lassen Sie uns der Sicherheit halber auf den Punkt kommen X 0-Funktion hat ein Maximum. Dann gilt für ausreichend kleine Inkremente Δ X wir haben f(x 0 + Δ X)
Übergabe dieser Ungleichungen an den Grenzwert bei Δ X→ 0 und unter Berücksichtigung der Ableitung F "(X 0) existiert, und daher hängt der Grenzwert links nicht davon ab, wie Δ X→ 0 erhalten wir: bei Δ X → 0 – 0 F"(X 0) ≥ 0 a bei Δ X → 0 + 0 F"(X 0) ≤ 0. Da F"(X 0) eine Zahl definiert, dann sind diese beiden Ungleichungen nur dann kompatibel, wenn F"(X 0) = 0.
Der bewährte Satz besagt, dass die Maximal- und Minimalpunkte nur zu den Werten des Arguments gehören können, bei denen die Ableitung Null wird.
Wir haben den Fall betrachtet, dass eine Funktion an allen Punkten eines bestimmten Segments eine Ableitung hat. Wie verhält es sich, wenn das Derivat nicht existiert? Schauen wir uns Beispiele an.
Beispiele.
- j=|X|.
Die Funktion hat an diesem Punkt keine Ableitung X=0 (an diesem Punkt hat der Graph der Funktion keinen definierten Tangens), aber an diesem Punkt hat die Funktion ein Minimum, da j(0)=0 und für alle X≠ 0j > 0.
- Lassen X< x
0 . Dann C< x
0 und f "(c)> 0.
Deshalb f "(c)(x- x 0)<
0 und daher
f(x) - f(x 0 )< 0, d.h. f(x)< f(x 0 ).
- Lassen x > x 0 . Dann c>x 0 und f "(c)< 0. Bedeutet f "(c)(x- x 0)< 0. Deshalb f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Finden Sie den Definitionsbereich einer Funktion f(x).
- Finden Sie die erste Ableitung einer Funktion f "(x).
- Bestimmen Sie hierfür kritische Punkte:
- Finden Sie die wahren Wurzeln der Gleichung f "(x)=0;
- Finden Sie alle Werte X für die die Ableitung f "(x) existiert nicht.
- Bestimmen Sie das Vorzeichen der Ableitung links und rechts vom kritischen Punkt. Da das Vorzeichen der Ableitung zwischen zwei kritischen Punkten konstant bleibt, reicht es aus, das Vorzeichen der Ableitung an einem Punkt links und einem Punkt rechts vom kritischen Punkt zu bestimmen.
- Berechnen Sie den Wert der Funktion an den Extrempunkten.
- Finden Sie alle kritischen Punkte der Funktion im Intervall ( a, b) und berechnen Sie die Werte der Funktion an diesen Punkten.
- Berechnen Sie die Werte der Funktion an den Enden des Segments, wenn x = a, x = b.
- Wählen Sie aus allen erhaltenen Werten den größten und den kleinsten aus.
Die Funktion hat keine Ableitung bei X=0, da es bei unendlich geht X=0. Aber an diesem Punkt hat die Funktion ein Maximum.

Die Funktion hat keine Ableitung bei X=0, da ![]() bei X→0. Zu diesem Zeitpunkt hat die Funktion weder ein Maximum noch ein Minimum. Wirklich, f(x)=0 und bei X<0f(x)<0, а при X>0f(x)>0.
bei X→0. Zu diesem Zeitpunkt hat die Funktion weder ein Maximum noch ein Minimum. Wirklich, f(x)=0 und bei X<0f(x)<0, а при X>0f(x)>0.

Aus den gegebenen Beispielen und dem formulierten Satz geht somit klar hervor, dass eine Funktion nur in zwei Fällen ein Extremum haben kann: 1) an Punkten, an denen die Ableitung existiert und gleich Null ist; 2) an dem Punkt, an dem die Ableitung nicht existiert.
Wenn jedoch irgendwann X 0 das wissen wir f "(x 0 ) =0, dann kann man hieraus nicht auf das schließen X 0 hat die Funktion ein Extremum.
Zum Beispiel. ![]() .
.

Aber Punkt X=0 ist kein Extrempunkt, da links von diesem Punkt die Funktionswerte unterhalb der Achse liegen Ochse, und rechts oben.
Es werden Werte eines Arguments aus dem Definitionsbereich einer Funktion aufgerufen, bei denen die Ableitung der Funktion verschwindet oder nicht existiert kritische Punkte.
Aus alledem folgt, dass die Extrempunkte der Funktion zu den kritischen Punkten gehören, allerdings ist nicht jeder kritische Punkt ein Extrempunkt. Um das Extremum einer Funktion zu ermitteln, müssen Sie daher alle kritischen Punkte der Funktion ermitteln und dann jeden dieser Punkte separat auf Maximum und Minimum untersuchen. Hierzu dient der folgende Satz.
Satz 2. (Ausreichende Bedingung für die Existenz eines Extremums.) Die Funktion sei in einem Intervall, das den kritischen Punkt enthält, stetig X 0 und ist an allen Punkten dieses Intervalls differenzierbar (außer vielleicht am Punkt selbst). X 0). Wenn bei der Bewegung von links nach rechts durch diesen Punkt die Ableitung das Vorzeichen von Plus nach Minus ändert, dann an diesem Punkt X = X 0-Funktion hat ein Maximum. Wenn, bei der Durchreise X 0 von links nach rechts ändert die Ableitung das Vorzeichen von Minus nach Plus, dann hat die Funktion an dieser Stelle ein Minimum.
Also, wenn
Nachweisen. Nehmen wir zunächst einmal an, dass es sich um eine Durchreise handelt X 0 ändert die Ableitung das Vorzeichen von Plus nach Minus, d.h. Vor allen X, nah am Punkt X 0 f "(x)> 0 für X< x 0 , f "(x)< 0 für x>x 0 . Wenden wir den Satz von Lagrange auf die Differenz an f(x) - f(x 0 ) = f "(c)(x- x 0), wo C liegt zwischen X Und X 0 .
Also für alle Werte X nah genug dran X 0 f(x)< f(x 0 ) . Und das bedeutet auf den Punkt gebracht X 0-Funktion hat ein Maximum.
Der zweite Teil des Minimumsatzes wird auf ähnliche Weise bewiesen.

Lassen Sie uns die Bedeutung dieses Theorems in der Abbildung veranschaulichen. Lassen f "(x 1 ) =0 und für alle X, nah genug dran X 1 sind die Ungleichungen erfüllt
f "(x)< 0 um X< x 1 , f "(x)> 0 um x>x 1 .
Dann links vom Punkt X 1 Die Funktion nimmt rechts zu und ab, also wann X = X 1 Funktion geht von steigend nach fallend, das heißt, sie hat ein Maximum.
Ebenso können wir Punkte berücksichtigen X 2 und X 3 .

Alles oben Genannte kann im Bild schematisch dargestellt werden:
Regel zum Studieren der Funktion y=f(x) für Extremum
Beispiele. Entdecken Sie die Funktionen für Minimum und Maximum.
MAXIMALE UND KLEINSTE WERTE EINER FUNKTION AUF EINEM Segment
Das größte Der Wert einer Funktion in einem Intervall ist der größte aller ihrer Werte in diesem Intervall und das kleinste– der kleinste aller seiner Werte.
Betrachten Sie die Funktion y=f(x) kontinuierlich auf dem Segment [ a, b]. Bekanntlich erreicht eine solche Funktion ihre Maximal- und Minimalwerte entweder am Rand des Segments oder innerhalb desselben. Wird der größte oder kleinste Wert einer Funktion an einem internen Punkt des Segments erreicht, dann ist dieser Wert das Maximum oder Minimum der Funktion, wird also an kritischen Punkten erreicht.
Somit erhalten wir Folgendes Regel zum Finden der größten und kleinsten Werte einer Funktion auf einem Segment[ a, b] :
Die Funktion $z=f(x,y)$ sei in einer Umgebung des Punktes $(x_0,y_0)$ definiert. Sie sagen, dass $(x_0,y_0)$ ein (lokaler) Maximalpunkt ist, wenn für alle Punkte $(x,y)$ in einer Umgebung des Punktes $(x_0,y_0)$ die Ungleichung $f(x,y) gilt ist befriedigt< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, dann heißt der Punkt $(x_0,y_0)$ der (lokale) Minimalpunkt.
Die Maximal- und Minimalpunkte werden oft allgemein als Extrempunkte bezeichnet.
Wenn $(x_0,y_0)$ ein Maximalpunkt ist, dann wird der Wert der Funktion $f(x_0,y_0)$ an diesem Punkt als Maximum der Funktion $z=f(x,y)$ bezeichnet. Dementsprechend wird der Wert der Funktion am Minimalpunkt als Minimum der Funktion $z=f(x,y)$ bezeichnet. Die Minima und Maxima einer Funktion werden durch einen gemeinsamen Term vereint – Extrema einer Funktion.
Algorithmus zur Untersuchung der Funktion $z=f(x,y)$ für Extremum
- Finden Sie die partiellen Ableitungen $\frac(\partial z)(\partial x)$ und $\frac(\partial z)(\partial y)$. Stellen Sie das Gleichungssystem $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0 zusammen und lösen Sie es . \ end(aligned) \right.$ Punkte, deren Koordinaten das angegebene System erfüllen, werden als stationär bezeichnet.
- Finden Sie $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ und berechnen Sie den Wert von $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left( \frac (\partial^2z)(\partial x\partial y) \right)^2$ an jedem stationären Punkt. Danach verwenden Sie das folgende Schema:
- Wenn $\Delta > 0$ und $\frac(\partial^2z)(\partial x^2) > 0$ (oder $\frac(\partial^2z)(\partial y^2) > 0$), dann ist der zu untersuchende Punkt der Mindestpunkt.
- Wenn $\Delta > 0$ und $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Wenn $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
- Wenn $\Delta = 0$, dann kann nichts Bestimmtes über das Vorhandensein eines Extremums gesagt werden; Es sind zusätzliche Untersuchungen erforderlich.
Hinweis (für ein vollständigeres Verständnis des Textes wünschenswert): Einblenden/Ausblenden
Wenn $\Delta > 0$, dann $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\ partiell^2z)(\partial x\partial y) \right)^2 > 0$. Und daraus folgt, dass $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) ( \partial x\partial y)\right)^2 ≥ 0$. Diese. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Ist das Produkt bestimmter Größen größer als Null, dann haben diese Größen das gleiche Vorzeichen. Das heißt zum Beispiel, wenn $\frac(\partial^2z)(\partial x^2) > 0$, dann ist $\frac(\partial^2z)(\partial y^2) > 0$. Kurz gesagt, wenn $\Delta > 0$, dann stimmen die Vorzeichen von $\frac(\partial^2z)(\partial x^2)$ und $\frac(\partial^2z)(\partial y^2)$ überein .
Beispiel Nr. 1
Untersuchen Sie die Funktion $z=4x^2-6xy-34x+5y^2+42y+7$ auf ihr Extremum.
$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$
$$ \left \( \begin(aligned) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(aligned) \right. $$
Reduzieren wir jede Gleichung dieses Systems um $2$ und verschieben wir die Zahlen auf die rechte Seite der Gleichungen:
$$ \left \( \begin(aligned) & 4x-3y=17;\\ & -3x+5y=-21. \end(aligned) \right. $$
Wir haben ein System linearer algebraischer Gleichungen erhalten. In dieser Situation erscheint es mir am bequemsten, die Cramer-Methode zur Lösung des resultierenden Systems zu verwenden.
$$ \begin(aligned) & \Delta=\left| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \& \Delta_x=\left| \begin(array) (cc) 17 & -3\\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \& \Delta_y=\left| \begin(array) (cc) 4 & 17\\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(aligned) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$
Die Werte $x=2$, $y=-3$ sind die Koordinaten des stationären Punktes $(2;-3)$.
$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$
Berechnen wir den Wert von $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$
Da $\Delta > 0$ und $\frac(\partial^2 z)(\partial x^2) > 0$, dann ist gemäß dem Punkt $(2;-3)$ der Minimalpunkt der Funktion $ z$. Wir finden das Minimum der Funktion $z$, indem wir die Koordinaten des Punktes $(2;-3)$ in die gegebene Funktion einsetzen:
$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3)+7=-90. $$
Antwort: $(2;-3)$ - Mindestpunktzahl; $z_(min)=-90$.
Beispiel Nr. 2
Untersuchen Sie die Funktion $z=x^3+3xy^2-15x-12y+1$ auf ihr Extremum.
Wir werden dem oben Gesagten folgen. Finden wir zunächst die partiellen Ableitungen erster Ordnung:
$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y)=6xy-12. $$
Erstellen wir ein Gleichungssystem $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( ausgerichtet) \right.$:
$$ \left \( \begin(aligned) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(aligned) \right. $$
Reduzieren wir die erste Gleichung um 3 und die zweite um 6.
$$ \left \( \begin(aligned) & x^2+y^2-5=0;\\ & xy-2=0. \end(aligned) \right. $$
Wenn $x=0$, dann führt uns die zweite Gleichung zu einem Widerspruch: $0\cdot y-2=0$, $-2=0$. Daher die Schlussfolgerung: $x\neq 0$. Dann haben wir aus der zweiten Gleichung: $xy=2$, $y=\frac(2)(x)$. Wenn wir $y=\frac(2)(x)$ in die erste Gleichung einsetzen, erhalten wir:
$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$
Wir haben eine biquadratische Gleichung. Wir führen die Ersetzung $t=x^2$ durch (was bedeutet, dass $t > 0$):
$$ t^2-5t+4=0;\\ \begin(aligned) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(aligned) $$
Wenn $t=1$, dann $x^2=1$. Daher haben wir zwei Werte von $x$: $x_1=1$, $x_2=-1$. Wenn $t=4$, dann ist $x^2=4$, d.h. $x_3=2$, $x_4=-2$. Wenn wir uns daran erinnern, dass $y=\frac(2)(x)$ ist, erhalten wir:
\begin(aligned) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\ & y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2)=-1. \end(ausgerichtet)
Wir haben also vier stationäre Punkte: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. Damit ist der erste Schritt des Algorithmus abgeschlossen.
Beginnen wir nun mit dem Algorithmus. Finden wir die partiellen Ableitungen zweiter Ordnung:
$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$
Finden wir $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$
Jetzt berechnen wir den Wert von $\Delta$ an jedem der zuvor gefundenen stationären Punkte. Beginnen wir am Punkt $M_1(1;2)$. An diesem Punkt haben wir: $\Delta(M_1)=36(1^2-2^2)=-108$. Da $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.
Lassen Sie uns den Punkt $M_2(-1;-2)$ untersuchen. An diesem Punkt haben wir: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Da $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.
Lassen Sie uns den Punkt $M_3(2;1)$ untersuchen. An diesem Punkt erhalten wir:
$$ \Delta(M_3)=36(2^2-1^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$
Da $\Delta(M_3) > 0$ und $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, dann ist gemäß $M_3(2; 1)$ ist der Minimalpunkt der Funktion $z$. Wir finden das Minimum der Funktion $z$, indem wir die Koordinaten des Punktes $M_3$ in die gegebene Funktion einsetzen:
$$ z_(min)=z(2;1)=2^3+3\cdot 2\cdot 1^2-15\cdot 2-12\cdot 1+1=-27. $$
Es bleibt noch der Punkt $M_4(-2;-1)$ zu untersuchen. An diesem Punkt erhalten wir:
$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$
Da $\Delta(M_4) > 0$ und $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1)+1=29. $$
Die Extremum-Studie ist abgeschlossen. Es bleibt nur noch, die Antwort aufzuschreiben.
Antwort:
- $(2;1)$ - Mindestpunkt, $z_(min)=-27$;
- $(-2;-1)$ – Maximalpunkt, $z_(max)=29$.
Notiz
Im allgemeinen Fall besteht keine Notwendigkeit, den Wert von $\Delta$ zu berechnen, da uns nur das Vorzeichen und nicht der spezifische Wert dieses Parameters interessiert. Zum Beispiel Nr. 2 oben betrachtet haben wir am Punkt $M_3(2;1)$ $\Delta=36\cdot(2^2-1^2)$. Hier ist offensichtlich, dass $\Delta > 0$ (da beide Faktoren $36$ und $(2^2-1^2)$ positiv sind) und es ist möglich, keinen bestimmten Wert von $\Delta$ zu finden. Für Standardberechnungen ist diese Bemerkung zwar nutzlos - dort müssen Sie die Berechnungen auf eine Zahl bringen :)
Beispiel Nr. 3
Untersuchen Sie die Funktion $z=x^4+y^4-2x^2+4xy-2y^2+3$ auf ihr Extremum.
Wir werden folgen. Finden wir zunächst die partiellen Ableitungen erster Ordnung:
$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$
Erstellen wir ein Gleichungssystem $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( ausgerichtet) \right.$:
$$ \left \( \begin(aligned) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(aligned) \right. $$
Reduzieren wir beide Gleichungen um $4$:
$$ \left \( \begin(aligned) & x^3-x+y=0;\\ & y^3+x-y=0. \end(aligned) \right. $$
Fügen wir die erste Gleichung zur zweiten hinzu und drücken $y$ durch $x$ aus:
$$ y^3+x-y+(x^3-x+y)=0;\\ y^3+x^3=0; y^3=-x^3; y=-x. $$
Wenn wir $y=-x$ in die erste Gleichung des Systems einsetzen, erhalten wir:
$$ x^3-x-x=0;\\ x^3-2x=0;\\ x(x^2-2)=0. $$
Aus der resultierenden Gleichung ergibt sich: $x=0$ oder $x^2-2=0$. Aus der Gleichung $x^2-2=0$ folgt, dass $x=-\sqrt(2)$ oder $x=\sqrt(2)$. Es werden also drei Werte von $x$ gefunden, nämlich: $x_1=0$, $x_2=-\sqrt(2)$, $x_3=\sqrt(2)$. Da $y=-x$, dann $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.
Der erste Schritt der Lösung ist abgeschlossen. Wir haben drei stationäre Punkte: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .
Beginnen wir nun mit dem Algorithmus. Finden wir die partiellen Ableitungen zweiter Ordnung:
$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$
Finden wir $\Delta$:
$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16\cdot((3x^2-1)(3y^2-1)-1). $$
Jetzt berechnen wir den Wert von $\Delta$ an jedem der zuvor gefundenen stationären Punkte. Beginnen wir am Punkt $M_1(0;0)$. An diesem Punkt haben wir: $\Delta(M_1)=16\cdot((3\cdot 0^2-1)(3\cdot 0^2-1)-1)=16\cdot 0=0$. Da $\Delta(M_1) = 0$ ist, sind zusätzliche Untersuchungen erforderlich, da über das Vorhandensein eines Extremums am betrachteten Punkt keine eindeutige Aussage getroffen werden kann. Lassen wir diesen Punkt vorerst beiseite und gehen wir zu anderen Punkten über.
Untersuchen wir den Punkt $M_2(-\sqrt(2),\sqrt(2))$. An diesem Punkt erhalten wir:
\begin(aligned) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2)=12\cdot (-\sqrt(2) )^2-4=24-4=20. \end(ausgerichtet)
Da $\Delta(M_2) > 0$ und $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, dann gilt gemäß $M_2(-\ sqrt(2),\sqrt(2))$ ist der Minimalpunkt der Funktion $z$. Wir finden das Minimum der Funktion $z$, indem wir die Koordinaten des Punktes $M_2$ in die gegebene Funktion einsetzen:
$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$
Ähnlich wie im vorherigen Punkt untersuchen wir den Punkt $M_3(\sqrt(2),-\sqrt(2))$. An diesem Punkt erhalten wir:
\begin(aligned) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1)=16\cdot 24=384;\\ & \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=12\cdot (\sqrt(2)) ^2-4=24-4=20. \end(ausgerichtet)
Da $\Delta(M_3) > 0$ und $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, dann ist gemäß $M_3(\sqrt (2),-\sqrt(2))$ ist der Minimalpunkt der Funktion $z$. Wir finden das Minimum der Funktion $z$, indem wir die Koordinaten des Punktes $M_3$ in die gegebene Funktion einsetzen:
$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2 ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$
Es ist Zeit, zum Punkt $M_1(0;0)$ zurückzukehren, an dem $\Delta(M_1) = 0$ ist. Demnach besteht weiterer Forschungsbedarf. Diese ausweichende Phrase bedeutet „mach, was du willst“ :). Es gibt keine allgemeine Lösung für solche Situationen, und das ist verständlich. Wenn es eine solche Methode gäbe, wäre sie längst in allen Lehrbüchern enthalten. In der Zwischenzeit müssen wir für jeden Punkt, an dem $\Delta = 0$ ist, nach einem speziellen Ansatz suchen. Schauen wir uns nun das Verhalten der Funktion in der Nähe des Punktes $M_1(0;0)$ an. Beachten wir sofort, dass $z(M_1)=z(0;0)=3$. Nehmen wir an, dass $M_1(0;0)$ der Mindestpunkt ist. Dann erhalten wir für jeden Punkt $M$ aus einer Umgebung des Punktes $M_1(0;0)$ $z(M) > z(M_1)$, d.h. $z(M) > 3$. Was ist, wenn eine Nachbarschaft Punkte enthält, an denen $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Betrachten wir Punkte, für die $y=0$, d.h. Punkte der Form $(x,0)$. An diesen Punkten nimmt die Funktion $z$ die folgenden Werte an:
$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2)+3. $$
In allen ausreichend kleinen Umgebungen $M_1(0;0)$ gilt $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Aber vielleicht ist der Punkt $M_1(0;0)$ der maximale Punkt? Wenn das so ist, dann erhalten wir für jeden Punkt $M$ aus einer Umgebung des Punktes $M_1(0;0)$ $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3$? Dann wird es am Punkt $M_1$ definitiv kein Maximum geben.
Betrachten wir Punkte, für die $y=x$, d.h. Punkte der Form $(x,x)$. An diesen Punkten nimmt die Funktion $z$ die folgenden Werte an:
$$ z(x,x)=x^4+x^4-2x^2+4x\cdot x-2\cdot x^2+3=2x^4+3. $$
Da in jeder Umgebung des Punktes $M_1(0;0)$ $2x^4 > 0$ gilt, dann ist $2x^4+3 > 3$. Schlussfolgerung: Jede Umgebung des Punktes $M_1(0;0)$ enthält Punkte, an denen $z > 3$, daher kann der Punkt $M_1(0;0)$ kein Maximalpunkt sein.
Der Punkt $M_1(0;0)$ ist weder ein Maximal- noch ein Minimalpunkt. Fazit: $M_1$ ist überhaupt kein Extrempunkt.
Antwort: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ sind die Mindestpunkte der Funktion $z$. An beiden Punkten $z_(min)=-5$.
Der Punkt x 0 heißt Maximalpunkt(Minimum) Funktion f(x), wenn in einer Umgebung des Punktes x 0 die Ungleichung f(x) ≤f(x 0) (f(x) ≥f(x 0)) erfüllt ist.
Der Wert der Funktion an dieser Stelle wird entsprechend aufgerufen maximal oder Minimum Funktionen. Die Maximum- und Minimum-Funktionen werden durch einen gemeinsamen Namen vereint Extremum Funktionen.
Das Extremum einer Funktion wird in diesem Sinne oft genannt lokales Extremum, wobei die Tatsache betont wird, dass dieses Konzept nur mit einer ausreichend kleinen Umgebung des Punktes x 0 verbunden ist. Auf demselben Intervall kann eine Funktion mehrere lokale Maxima und Minima haben, die nicht unbedingt übereinstimmen globales Maximum oder Minimum(d. h. der größte oder kleinste Wert der Funktion über das gesamte Intervall).
Notwendige Bedingung für Extremum. Damit eine Funktion an einem Punkt ein Extremum hat, muss ihre Ableitung an diesem Punkt gleich Null sein oder nicht existieren.
Für differenzierbare Funktionen folgt diese Bedingung aus dem Satz von Fermat. Darüber hinaus wird auch der Fall berücksichtigt, dass eine Funktion an einem Punkt ein Extremum hat, an dem sie nicht differenzierbar ist.
Die Punkte, an denen die notwendige Extremumbedingung erfüllt ist, werden aufgerufen kritisch(oder stationär für eine differenzierbare Funktion). Diese Punkte müssen innerhalb des Funktionsbereichs liegen.
Wenn es also an irgendeinem Punkt ein Extremum gibt, dann ist dieser Punkt kritisch (notwendige Bedingung). Beachten Sie, dass das Gegenteil nicht der Fall ist. Der kritische Punkt ist nicht unbedingt ein Extrempunkt, d. h. die angegebene Bedingung ist nicht ausreichend.
Die erste hinreichende Bedingung für ein Extremum. Wenn die Ableitung der differenzierbaren Funktion beim Durchgang durch einen bestimmten Punkt ihr Vorzeichen von Plus nach Minus ändert, dann ist dies der Maximalpunkt der Funktion, und wenn von Minus nach Plus, dann ist dies der Minimalpunkt.
Der Beweis dieser Bedingung folgt aus der hinreichenden Bedingung der Monotonie (wenn sich das Vorzeichen der Ableitung ändert, findet ein Übergang entweder von einer Zunahme der Funktion zu einer Abnahme oder von einer Abnahme zu einer Zunahme statt).
Die zweite hinreichende Bedingung für ein Extremum. Wenn die erste Ableitung einer zweimal differenzierbaren Funktion an einem Punkt Null ist und die zweite Ableitung an diesem Punkt positiv ist, dann ist dies der Minimalpunkt der Funktion; und wenn die zweite Ableitung negativ ist, dann ist dies der Maximalpunkt.
Der Beweis dieser Bedingung basiert ebenfalls auf der hinreichenden Bedingung der Monotonie. Wenn die zweite Ableitung positiv ist, ist die erste Ableitung tatsächlich eine steigende Funktion. Da es an dem betreffenden Punkt gleich Null ist, ändert es beim Durchgang durch ihn das Vorzeichen von Minus nach Plus, was uns zur ersten hinreichenden Bedingung für ein lokales Minimum zurückführt. Wenn die zweite Ableitung negativ ist, nimmt die erste ab und ändert das Vorzeichen von Plus nach Minus, was eine ausreichende Bedingung für ein lokales Maximum ist.
Untersuchung einer Funktion für ein Extremum umfasst gemäß den formulierten Theoremen folgende Phasen:
1. Finden Sie die erste Ableitung der Funktion f`(x).
2. Überprüfen Sie die Erfüllung der notwendigen Extremumbedingung, d. h. Finden Sie die kritischen Punkte der Funktion f(x), an denen die Ableitung f`(x) = 0 ist oder nicht existiert.
3. Überprüfen Sie die Erfüllung der hinreichenden Bedingung für das Extremum, d. h. Untersuchen Sie entweder das Vorzeichen der Ableitung links und rechts von jedem kritischen Punkt oder finden Sie die zweite Ableitung f``(x) und bestimmen Sie ihr Vorzeichen an jedem kritischen Punkt. Ziehen Sie eine Schlussfolgerung über das Vorhandensein von Extrema der Funktion.
4. Finden Sie die Extrema (Extremwerte) der Funktion.
Ermitteln des globalen Maximums und Minimums einer Funktionüber einen gewissen Zeitraum hat es auch große praktische Bedeutung. Die Lösung dieses Problems auf einem Segment basiert auf dem Satz von Weierstrass, nach dem eine stetige Funktion auf einem Segment ihren größten und kleinsten Wert annimmt. Sie können sowohl an Extrempunkten als auch an den Enden des Segments erreicht werden. Daher umfasst die Lösung die folgenden Schritte:
1. Finden Sie die Ableitung der Funktion f`(x).
2. Finden Sie die kritischen Punkte der Funktion f(x), an denen die Ableitung f`(x) = 0 ist oder nicht existiert.
3. Finden Sie die Werte der Funktion an kritischen Punkten und an den Enden des Segments und wählen Sie daraus den größten und den kleinsten aus.
Dies ist ein ziemlich interessanter Bereich der Mathematik, der absolut allen Absolventen und Studenten begegnet. Allerdings mag nicht jeder Matan. Manche können nicht einmal grundlegende Dinge wie eine scheinbar standardmäßige Funktionsstudie verstehen. Dieser Artikel soll ein solches Versäumnis korrigieren. Möchten Sie mehr über Funktionsanalyse erfahren? Möchten Sie wissen, was Extrempunkte sind und wie man sie findet? Dann ist dieser Artikel genau das Richtige für Sie.
Den Graphen einer Funktion studieren
Zunächst lohnt es sich zu verstehen, warum Sie das Diagramm überhaupt analysieren müssen. Es gibt einfache Funktionen, die nicht schwer zu zeichnen sind. Ein markantes Beispiel für eine solche Funktion ist eine Parabel. Es wird nicht schwierig sein, eine Grafik zu zeichnen. Es genügt, mit einer einfachen Transformation die Zahlen zu finden, bei denen die Funktion den Wert 0 annimmt. Und im Prinzip ist das alles, was Sie wissen müssen, um einen Graphen einer Parabel zu zeichnen.
Was aber, wenn die Funktion, die wir grafisch darstellen müssen, viel komplexer ist? Da die Eigenschaften komplexer Funktionen nicht ganz offensichtlich sind, ist eine umfassende Analyse erforderlich. Erst danach kann die Funktion grafisch dargestellt werden. Wie macht man das? Die Antwort auf diese Frage finden Sie in diesem Artikel.
Funktionsanalyseplan
Das erste, was wir tun müssen, ist eine oberflächliche Untersuchung der Funktion, bei der wir den Definitionsbereich finden. Beginnen wir also der Reihe nach. Der Definitionsbereich ist die Wertemenge, durch die die Funktion definiert wird. Einfach ausgedrückt sind dies die Zahlen, die in einer Funktion anstelle von x verwendet werden können. Um den Umfang zu bestimmen, genügt ein Blick in die Akte. Es ist beispielsweise offensichtlich, dass die Funktion y (x) = x 3 + x 2 - x + 43 einen Definitionsbereich hat, der die Menge der reellen Zahlen ist. Nun, bei einer Funktion wie (x 2 - 2x)/x ist alles etwas anders. Da die Zahl im Nenner nicht gleich 0 sein darf, umfasst der Definitionsbereich dieser Funktion alle reellen Zahlen außer Null.
Als nächstes müssen Sie die sogenannten Nullstellen der Funktion finden. Dies sind die Argumentwerte, bei denen die gesamte Funktion den Wert Null annimmt. Dazu ist es notwendig, die Funktion mit Null gleichzusetzen, sie im Detail zu betrachten und einige Transformationen durchzuführen. Nehmen wir die bereits bekannte Funktion y(x) = (x 2 - 2x)/x. Aus dem Schulunterricht wissen wir, dass ein Bruch gleich 0 ist, wenn der Zähler gleich Null ist. Deshalb verwerfen wir den Nenner und beginnen mit dem Zähler zu arbeiten, indem wir ihn mit Null gleichsetzen. Wir erhalten x 2 - 2x = 0 und setzen x aus Klammern. Daher ist x (x - 2) = 0. Als Ergebnis stellen wir fest, dass unsere Funktion gleich Null ist, wenn x gleich 0 oder 2 ist.
Bei der Untersuchung des Graphen einer Funktion stoßen viele Menschen auf Probleme in Form von Extrempunkten. Und es ist seltsam. Extreme sind schließlich ein recht einfaches Thema. Glauben Sie mir nicht? Überzeugen Sie sich selbst, indem Sie diesen Teil des Artikels lesen, in dem wir über Mindest- und Höchstpunkte sprechen.

Zunächst lohnt es sich zu verstehen, was ein Extremum ist. Ein Extremum ist der Grenzwert, den eine Funktion in einem Diagramm erreicht. Es stellt sich heraus, dass es zwei Extremwerte gibt – Maximum und Minimum. Zur Verdeutlichung können Sie sich das Bild oben ansehen. Im untersuchten Gebiet ist Punkt -1 das Maximum der Funktion y (x) = x 5 - 5x und Punkt 1 dementsprechend das Minimum.
Verwechseln Sie die Konzepte auch nicht. Die Extrempunkte einer Funktion sind die Argumente, an denen eine gegebene Funktion Extremwerte annimmt. Das Extremum wiederum ist der Wert der Minima und Maxima einer Funktion. Betrachten Sie zum Beispiel noch einmal die obige Abbildung. -1 und 1 sind die Extrempunkte der Funktion und 4 und -4 sind die Extrempunkte selbst.
Extrempunkte finden

Aber wie findet man die Extrempunkte einer Funktion? Alles ist ganz einfach. Als Erstes muss die Ableitung der Gleichung ermittelt werden. Nehmen wir an, wir haben die Aufgabe erhalten: „Finden Sie die Extrempunkte der Funktion y (x), x ist das Argument. Zur Verdeutlichung nehmen wir die Funktion y (x) = x 3 + 2x 2 + x + 54. Lassen Sie uns differenzieren und.“ erhalten Sie die folgende Gleichung: 3x 2 + 4x + 1. Als Ergebnis haben wir eine quadratische Standardgleichung. Als nächstes müssen wir sie nur noch mit Null gleichsetzen und die Wurzeln finden. Da die Diskriminante größer als Null ist (D = 16 - 12 = 4) wird diese Gleichung durch zwei Wurzeln bestimmt. Finden Sie sie und erhalten Sie zwei Werte: 1/3 und -1. Dies sind die Extrempunkte der Funktion. Wie können Sie jedoch trotzdem bestimmen, wer wer ist? Welcher Punkt ist das Maximum und welcher das Minimum? Dazu müssen Sie den Nachbarpunkt nehmen und seinen Wert ermitteln. Nehmen Sie beispielsweise die Zahl -2, die sich links entlang der Koordinatenlinie von -1 befindet . Setzen Sie diesen Wert in unsere Gleichung ein y(-2) = 12 - 8 + 1 = 5. Als Ergebnis erhalten wir eine positive Zahl. Dies bedeutet, dass im Intervall von Die Funktion steigt von 1/3 auf -1. Dies bedeutet wiederum, dass die Funktion in den Intervallen von minus Unendlich bis 1/3 und von -1 bis plus Unendlich abnimmt. Daraus können wir schließen, dass die Zahl 1/3 der Minimalpunkt der Funktion im untersuchten Intervall und -1 der Maximalpunkt ist.

Es ist auch erwähnenswert, dass das Einheitliche Staatsexamen nicht nur das Finden von Extrempunkten erfordert, sondern auch die Durchführung einer Operation mit ihnen (Addieren, Multiplizieren usw.). Aus diesem Grund lohnt es sich, den Bedingungen des Problems besondere Aufmerksamkeit zu schenken. Denn durch Unaufmerksamkeit kann man Punkte verlieren.